Next: Sample Test Problems Up: The Radial Equation and Previous: Scattering from a Spherical Contents
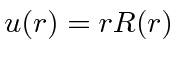 *
*
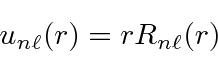
![\begin{eqnarray*}
\left({d^2\over dr^2}+{2\over r}{d\over dr}\right){u(r)\over r...
...left[E-V(r)-{\ell(\ell+1)\hbar^2\over 2\mu r^2}\right]u(r)=0 \\
\end{eqnarray*}](img1928.png)
We do get the additional condition that
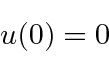
For the case of a constant potential
![]() , we define
, we define
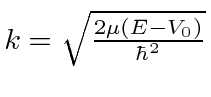 and
and
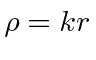 ,
and the radial equation becomes.
,
and the radial equation becomes.
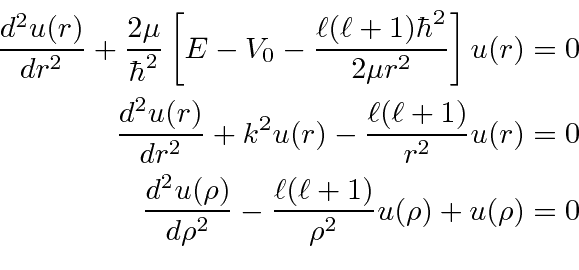
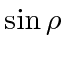 and
and
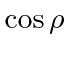 are solutions.
Dividing by
are solutions.
Dividing by
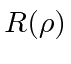 , we see that these are
, we see that these are
Jim Branson 2013-04-22