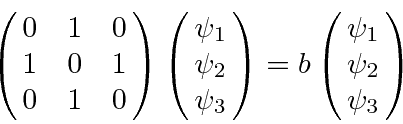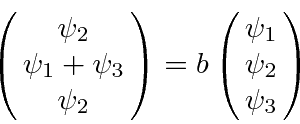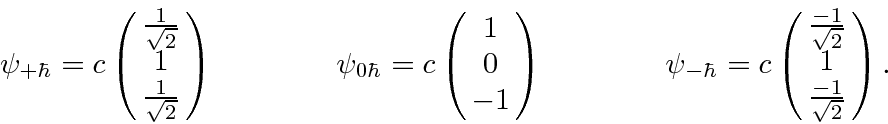Eigenvectors of
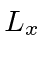
We will do it as if we don't already
know that the eigenvalues are
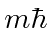 .
.
where
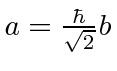 .
.
There are three solutions to this equation:
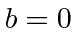 ,
,
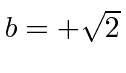 , and
, and
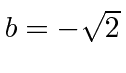 or
or
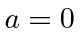 ,
,
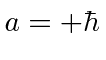 , and
, and
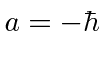 .
These are the eigenvalues we expected for
.
These are the eigenvalues we expected for
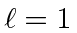 .
For each of these three eigenvalues, we should go back and find the
corresponding eigenvector by using the matrix equation.
.
For each of these three eigenvalues, we should go back and find the
corresponding eigenvector by using the matrix equation.
Up to a normalization constant, the solutions are:
We should normalize these eigenvectors to represent one particle.
For example:
Try calculating the eigenvectors of 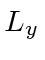 .
.
You already know what the eigenvalues are.
Jim Branson
2013-04-22
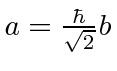 .
.
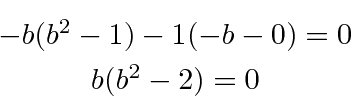
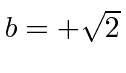 , and
, and
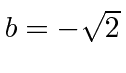 or
or
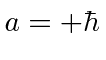 , and
, and
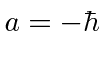 .
These are the eigenvalues we expected for
.
These are the eigenvalues we expected for