Next: Review of the Classical Up: Quantum Physics 130 Previous: Homework 9 Contents
In this section, we will study the interactions of electrons in an electromagnetic field. We will compute the additions to the Hamiltonian for magnetic fields. The gauge symmetry exhibited in electromagnetism will be examined in quantum mechanics. We will show that a symmetry allowing us to change the phase of the electron wave function requires the existence of EM interactions (with the gauge symmetry).
These topics are covered in Gasiorowicz Chapter 13,
and in Cohen-Tannoudji et al. Complements 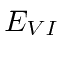 ,
, 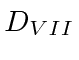 and
and 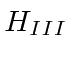 .
.