Next: The Lorentz Force from Up: Derivations and Computations Previous: Derivations and Computations Contents
We take Maxwell's equations and the fields written in terms of the potentials as input.
In the left column the equations are given in the standard form while the right column gives the equivalent equation in terms of indexed components.
The right column uses the totally antisymmetric tensor in 3D
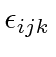 and assumes summation over repeated indices (Einstein notaton).
So in this notation, dot products can be simply written as
and assumes summation over repeated indices (Einstein notaton).
So in this notation, dot products can be simply written as
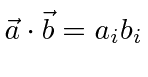 and any component of a cross product is written
and any component of a cross product is written
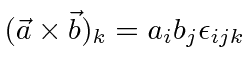 .
.
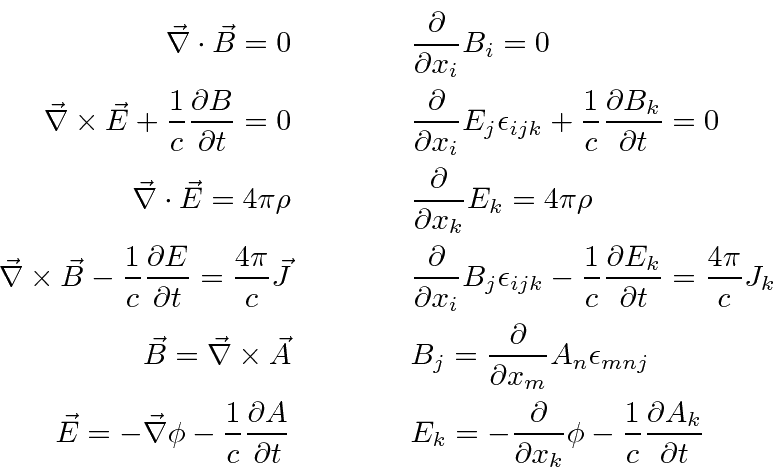
If the fields are written in terms of potentials, then the first two Maxwell equations are automatically satisfied.
Lets verify the first equation by plugging in the B field in terms of the potential and noticing that we can interchange
the order of differentiation.
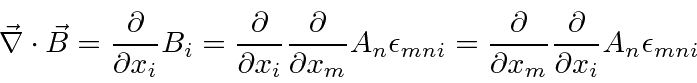
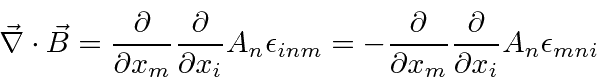
For the second equation, we write it out in terms of the potentials and notice that the first term
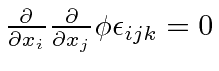 for the same reason as above.
for the same reason as above.
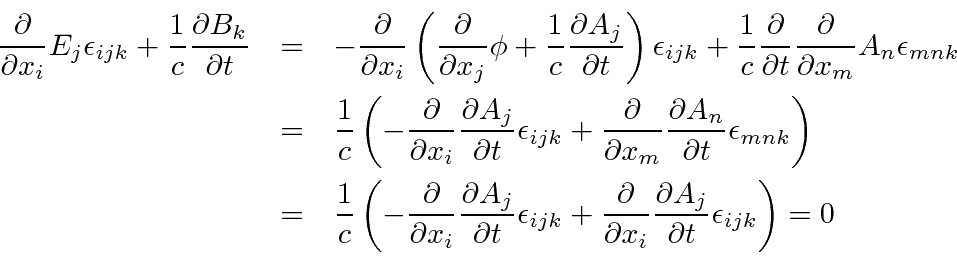
Similarly we may work with the Gauss's law equation
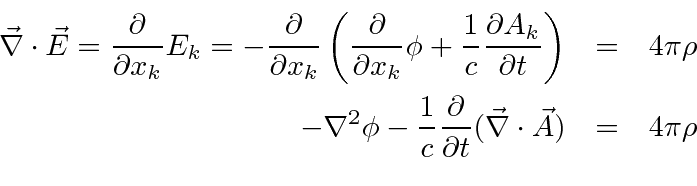
For the fourth equation we have.
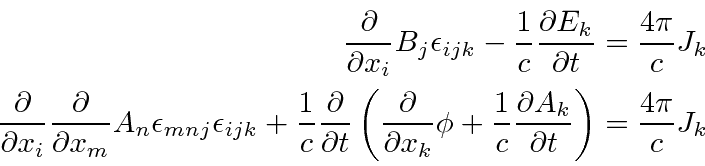
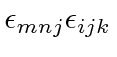 as occurs above.
All the indices of any tensor have to be different in order to get a nonzero result.
Since the
as occurs above.
All the indices of any tensor have to be different in order to get a nonzero result.
Since the
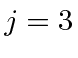 so the other 2 terms in the sum are zero.
But if
so the other 2 terms in the sum are zero.
But if
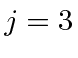 , we must have either
, we must have either
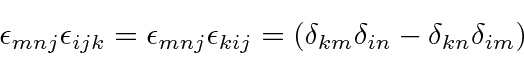
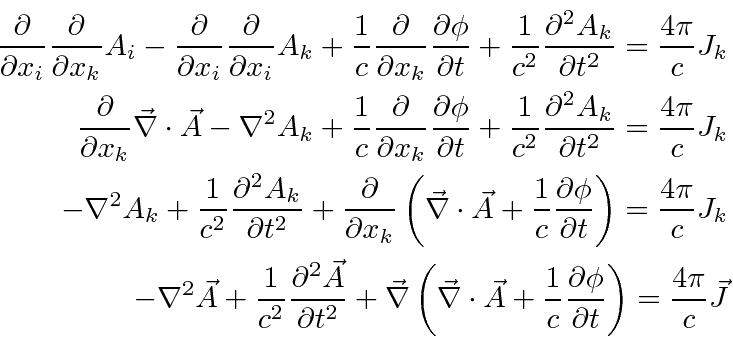
The last two equations derived are wave equations with source terms obeyed by the potentials. As discussed in the opening section of this chapter, they can be simplified with a choice of gauge.
Jim Branson 2013-04-22