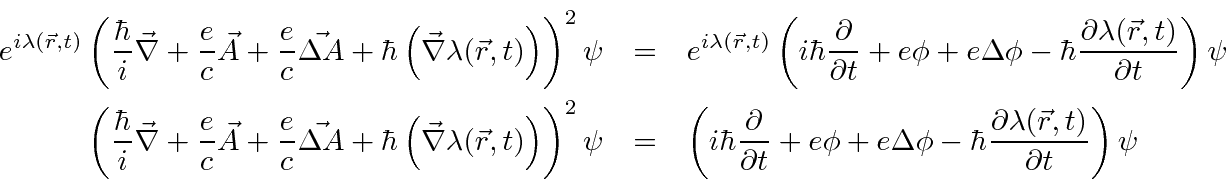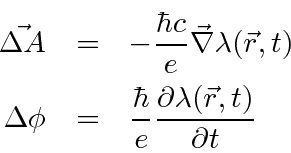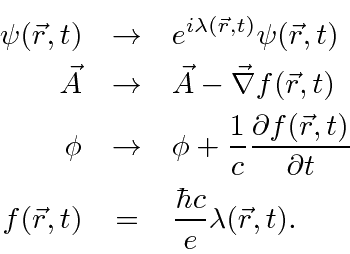A Hamiltonian Invariant Under Wavefunction Phase (or Gauge) Transformations
We want to investigate what it takes for the
Hamiltonian to be invariant under a local phase
transformation
of the wave function.
That is, we can change the phase by a different amount at each point in spacetime and
the physics will remain unchanged.
We know that the absolute square of the wavefunction is the same.
The Schrödinger must also be unchanged.
So let's
postulate the following transformation
then see what we need to keep the equation invariant.
We now need to apply this transformation to the Schrödinger equation.
Now we will
apply the differential operator to the exponential
to identify the new terms.
Note that
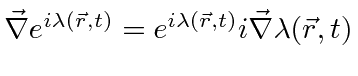 .
.
Its easy to see that we can
leave this equation invariant with the following choices.
We can argue that we need Electromagnetism to give us the local phase transformation symmetry
for electrons.
We now rewrite the gauge transformation in the more conventional way, the convention being set
before quantum mechanics.
Jim Branson
2013-04-22
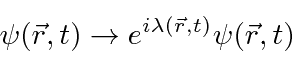
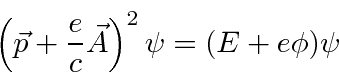
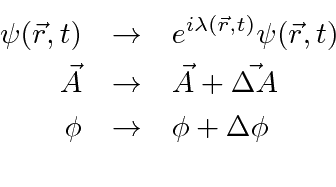
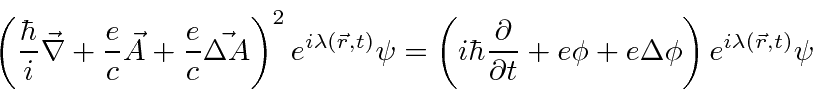
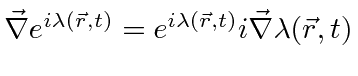 .
.