Next: Homework Problems Up: Derivations and Computations Previous: A Hamiltonian Invariant Under Contents
We've shown that we can compute the function
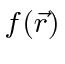 from the vector potential.
from the vector potential.
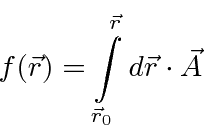
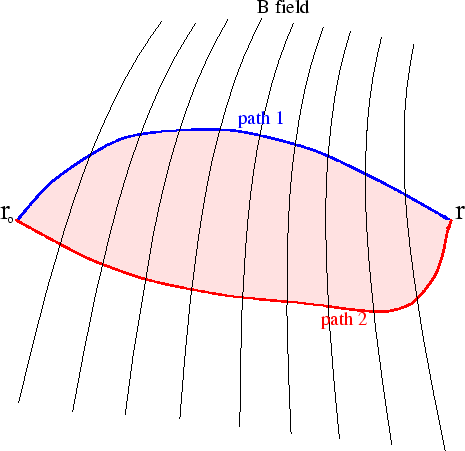
Consider two different paths from
![]() to
to
![]() .
.
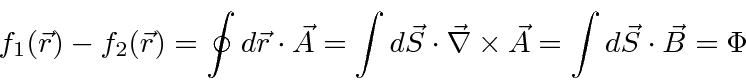
Now
![]() is not a physical observable so the
is not a physical observable so the
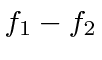 does not have to be zero, but,
does not have to be zero, but,
![]() does have to
be single valued.
does have to
be single valued.
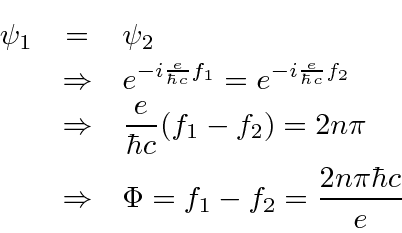
Magnetic flux is observed to be quantized in a region enclosed by a superconductor.
however, the fundamental charge seen is
![]() .
.
Jim Branson 2013-04-22