Next: Sample Test Problems Up: Electrons in an Electromagnetic Previous: Magnetic Flux Quantization from Contents
![$H={1\over 2\mu}[\vec{p}+{e\over c}\vec{A}(\vec{r},t)]^2-e\phi(\vec{r},t)$](img2752.png) yields the Lorentz force law for an electron. Note that the fields must
be evaluated at the position of the electron. This means that the total
time derivative of
yields the Lorentz force law for an electron. Note that the fields must
be evaluated at the position of the electron. This means that the total
time derivative of
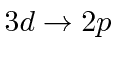 transition in Hydrogen atoms in a
transition in Hydrogen atoms in a
![\begin{displaymath}H={1\over 2\mu}[\vec{p}+{e\over c}\vec{A}]^2\end{displaymath}](img2755.png)
![\begin{displaymath}\vec{j}={\hbar\over 2i\mu}[\psi^*\vec{\nabla}\psi-
(\vec{\nabla}\psi^*)\psi+{2ie\over \hbar c}\vec{A}\psi^*\psi].\end{displaymath}](img2756.png)
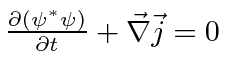 .
.
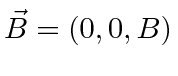 with the gauge chosen so that
with the gauge chosen so that
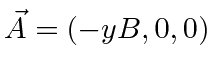 .
What are the constants of the motion?
Go as far as you can in solving the equations of motion
and obtain the energy spectrum.
Can you explain why the same problem in the gauges
.
What are the constants of the motion?
Go as far as you can in solving the equations of motion
and obtain the energy spectrum.
Can you explain why the same problem in the gauges
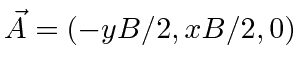 and
and
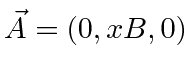 can represent the same physical situation?
Why do the solutions look so different?
can represent the same physical situation?
Why do the solutions look so different?
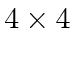 corner of the matrix representation of
corner of the matrix representation of
![$H={1\over 2m}[\vec{p}+{e\over c}\vec{A}(\vec{r},t)]^2-e\phi(\vec{r},t)
+{e\hbar\over 2mc}\vec{\sigma}\cdot\vec{B(\vec{r},t)}$](img2764.png) .
Show that this can be written as the Pauli Hamiltonian
.
Show that this can be written as the Pauli Hamiltonian
![\begin{displaymath}H={1\over 2m}\left(\vec{\sigma}\cdot[\vec{p}+{e\over c}\vec{A}(\vec{r},t)]\right)^2-e\phi(\vec{r},t).\end{displaymath}](img2765.png)
Jim Branson 2013-04-22