Energy States of Electrons in a Plasma II

We are going to solve the same plasma in a constant B field in a different gauge. If 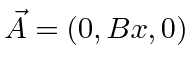$\vec{A}=\left(0,Bx,0\right)$, then

$$\bgroup\color{black}\vec{B}=\vec\nabla\times\vec{A}={\partial A_y\over{\partial x}}\hat{z}=B\hat{z}.\egroup$$

This $A$ gives us the same B field. We can then compute H for a constant B field in the z direction.

$$\begin{eqnarray*} H & = & {1\over {2 m_e}}\left(\vec{p}+{e\over c}\vec{A}\right)... ...{2eB\over c}x p_y + \left(eB\over c\right)^2 x^2 + p^2_z\right) \end{eqnarray*}$$

With this version of the same problem, we have

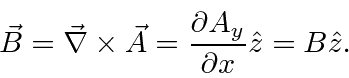
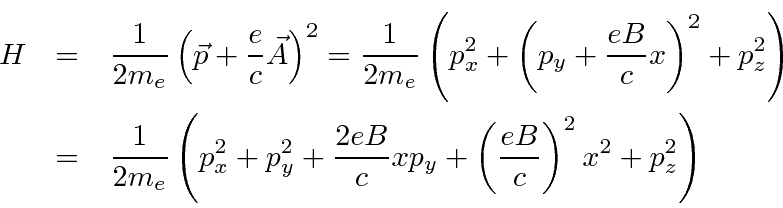
$$\bgroup\color{black}\left[H,p_y\right]=\left[H,p_z\right]=0.\egroup$$

We can treat $p_z$ and $p_y$ as constants of the motion and solve the problem in Cartesian coordinates!The terms in $x$ and $p_y$ are actually a perfect square.

$$\bgroup\color{black}\psi=v(x)e^{ik_yy}e^{ik_zz}\egroup$$

$$\begin{eqnarray*} {1\over {2 m_e}}\left(-\hbar^2{d^2\over{dx^2}} + \left(eB\ove... ...t)^2\right)v(x) &=&\left(E-{\hbar^2k_z^2\over 2 m_e}\right)v(x) \end{eqnarray*}$$

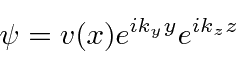
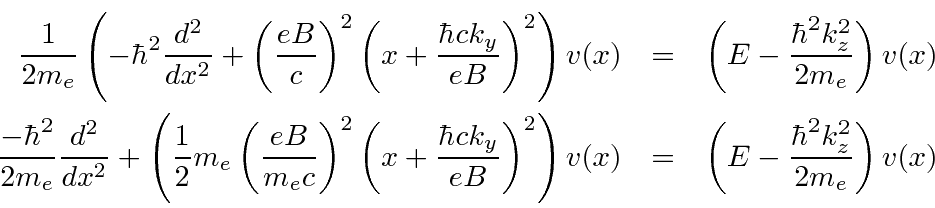
This is the same as the 1D harmonic oscillator equation with 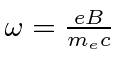$\omega={eB\over{ m_e c}}$ and $x_0=-{\hbar c k\over{eB}}$.

$$\bgroup\color{black}E=\left(n+{1\over 2}\right)\hbar\omega={\... ...c}}\left(n+{1\over 2}\right) +{\hbar^2k_z^2\over 2 m_e}\egroup$$

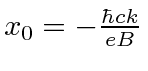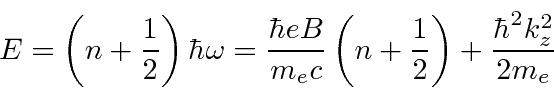
So we get the same energies with a much simpler calculation. The resulting states are somewhat strange and are not analogous to the classical solutions. (Note that an electron could be circulating about any field line so there are many possible states, just in case you are worrying about the choice of $k_y$ and $x_0$ and counting states.)