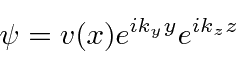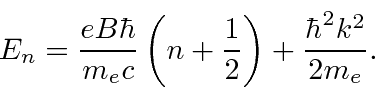A Plasma in a Magnetic Field
An important place where both magnetic terms come into play is in a plasma.There, many electrons are not bound to atoms and external Electric fields are screened out.
Let's assume there is a constant (enough) B field in the z direction.
We then have cylindrical symmetry and will work in the coordinates,
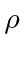 ,
,
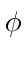 , and
, and
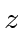 .
.
The problem clearly has translational symmetry along the z direction and
rotational symmetry around the z axis.
Given the symmetry, we know that
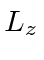 and
and
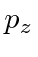 commute with the Hamiltonian and will give
constants of the motion. We therefore will be able to separate variables in the usual way.
commute with the Hamiltonian and will give
constants of the motion. We therefore will be able to separate variables in the usual way.
In solving
the equation in
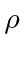 we may reuse the Hydrogen solution ultimately
get the energies
we may reuse the Hydrogen solution ultimately
get the energies
and associated LaGuerre polynomials (as in Hydrogen) in
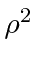 (instead of
(instead of
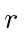 ).
).
The solution turns out to be
simpler using the Hamiltonian written in terms of
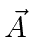 if we choose the right gauge by setting
if we choose the right gauge by setting
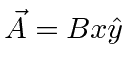 .
.
This Hamiltonian does not depend on
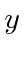 or
or
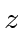 and therefore has
translational symmetry in both x and y so their conjugate momenta are conserved.
We can use this symmetry to write the solution and reduce to a 1D equation in
and therefore has
translational symmetry in both x and y so their conjugate momenta are conserved.
We can use this symmetry to write the solution and reduce to a 1D equation in
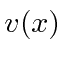 .
.
Then we actually can use our harmonic oscillator solution instead of hydrogen!
The energies come out to be
Neglecting the free particle behavior in
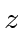 , these are called the Landau Levels.This is an example of the equivalence of the two real problems we know how to solve.
, these are called the Landau Levels.This is an example of the equivalence of the two real problems we know how to solve.
Jim Branson
2013-04-22
![]() ,
,
![]() , and
, and
![]() .
.
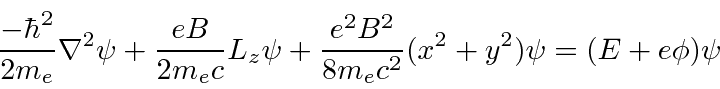
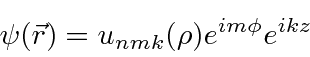
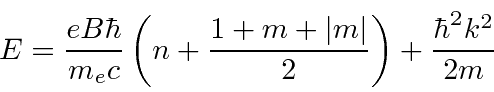
![]() if we choose the right gauge by setting
if we choose the right gauge by setting
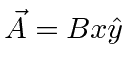 .
.
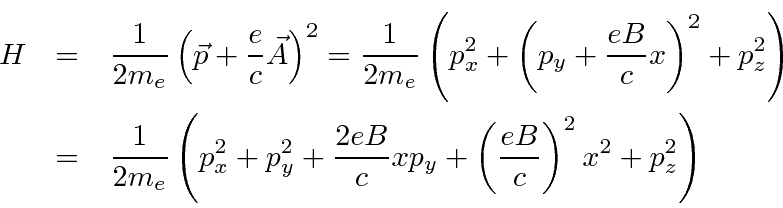
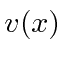 .
.