Next: A Plasma in a Up: Examples Previous: Examples Contents
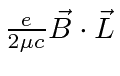 .
Choosing the z axis so that the constant field points in the z direction, we have
.
Choosing the z axis so that the constant field points in the z direction, we have
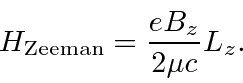
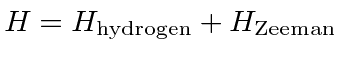 .
Remember, our hydrogen states are eigenstates of H,
.
Remember, our hydrogen states are eigenstates of H,
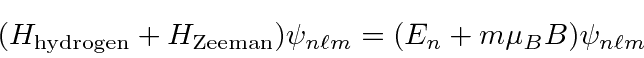
This would be a really nice tool to study the number of degenerate states in each hydrogen level. When the experiment was done, things did not work our according to plan at all. The magnetic moment of the electron' s spin greatly complicates the problem. We will solve this later.
Jim Branson 2013-04-22