Next: Examples Up: Electrons in an Electromagnetic Previous: The Quantum Hamiltonian Including Contents
Gauge symmetry in Electromagnetism was recognized before the advent of quantum mechanics. We have seen that symmetries play a very important role in the quantum theory. Indeed, in quantum mechanics, gauge symmetry can be seen as the basis for electromagnetism and conservation of charge.
We know that the all observables are unchanged if we make a global change of the
phase of the wavefunction,
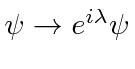 .
We could call this global phase symmetry.All relative phases (say for amplitudes to go through different slits in a diffraction
experiment) remain the same and no physical observable changes.
This is a symmetry in the theory which we already know about.
Let's postulate that there is a bigger symmetry and see what the consequences are.
.
We could call this global phase symmetry.All relative phases (say for amplitudes to go through different slits in a diffraction
experiment) remain the same and no physical observable changes.
This is a symmetry in the theory which we already know about.
Let's postulate that there is a bigger symmetry and see what the consequences are.
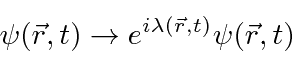
Its clear that this transformation leaves
the absolute square of the wavefunction the same,
but what about the
Schrödinger equation?
It must also be unchanged.
The derivatives in the Schrödinger equation
will act on
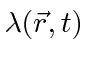 changing the equation
unless we do something else to cancel the changes.
changing the equation
unless we do something else to cancel the changes.
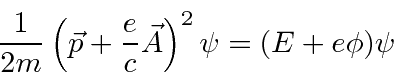
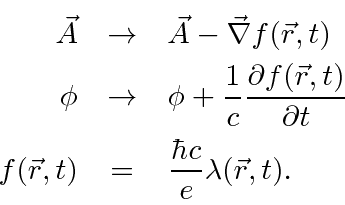
This is just the standard gauge transformation of electromagnetism, but, we now see that local phase symmetry of the wavefunction requires gauge symmetry for the fields and indeed even requires the existence of the EM fields to cancel terms in the Schrödinger equation. Electromagnetism is called a gauge theory because the gauge symmetry actually defines the theory. It turns out that the weak and the strong interactions are also gauge theories and, in some sense, have the next simplest possible gauge symmetries after the one in Electromagnetism.
We will write our standard gauge transformation in the traditional way to conform a bit better to the textbooks.
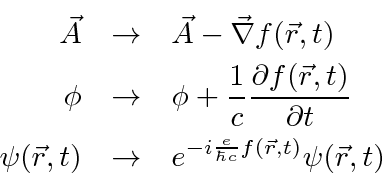
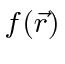 .
To be specific, take our gauge transformation of the vector potential.
Make a gauge transformation such that
.
To be specific, take our gauge transformation of the vector potential.
Make a gauge transformation such that
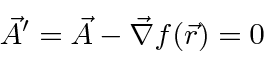
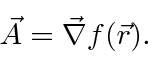
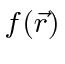 in terms of
in terms of
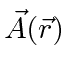 .
.
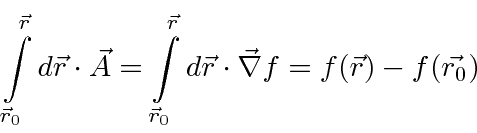
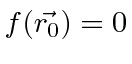 , then we have a
very useful relation between the gauge function and the vector potential in a field free region.
, then we have a
very useful relation between the gauge function and the vector potential in a field free region.
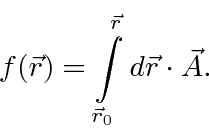
We can derive
the quantization of magnetic flux
by calculating the line integral of
![]() around a closed loop in a field free region.
around a closed loop in a field free region.
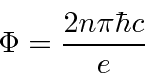
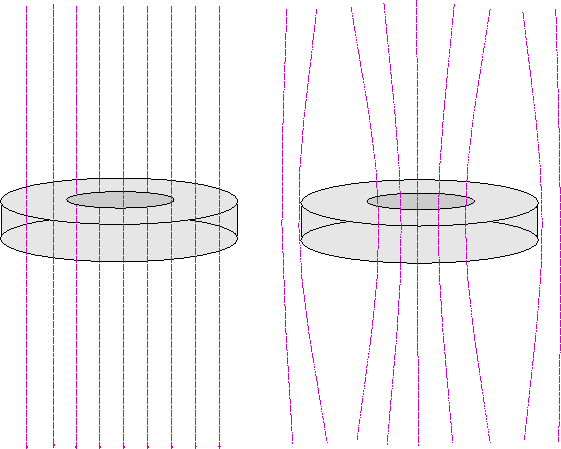
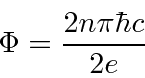
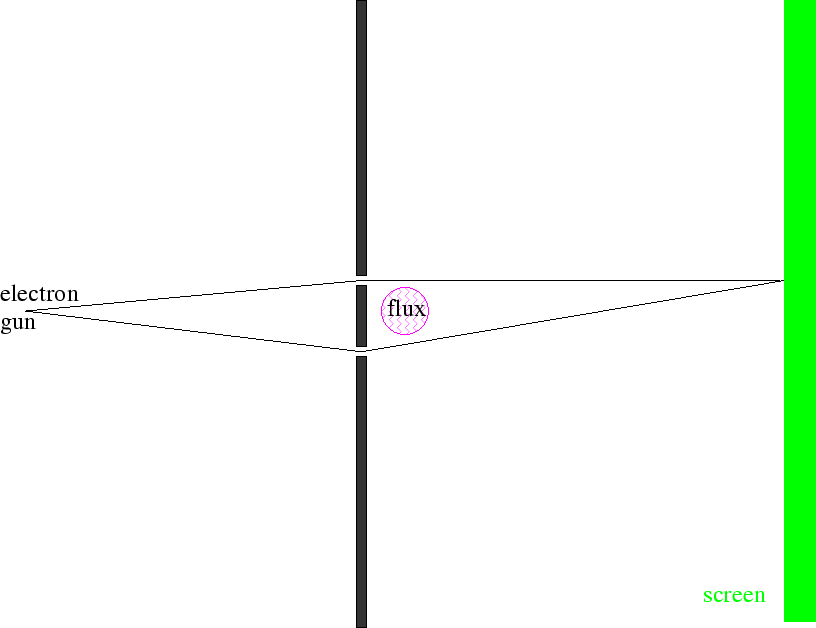
The Aharanov Böhm Effect brings us back to the two slit diffraction experiment but adds magnetic fields.
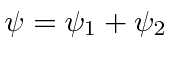 .
Let's start with
.
Let's start with
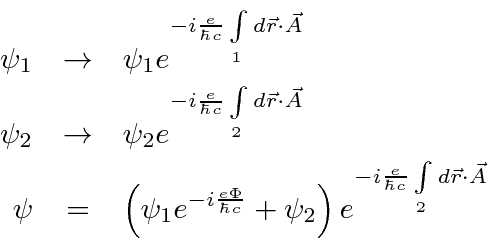
Jim Branson 2013-04-22