Next: About this document ... Up: Quantum Physics 130 Previous: Homework Problems Contents
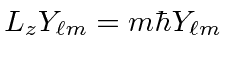
|
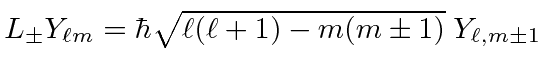
|
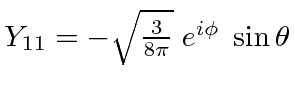 |
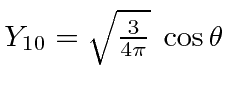
|
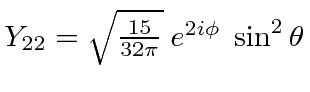
|
|
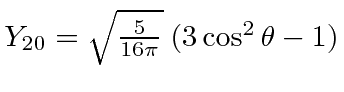
|
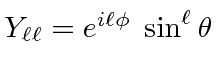
|
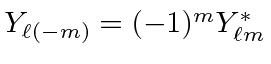 |
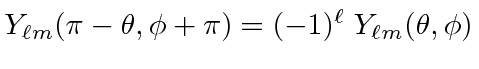
|
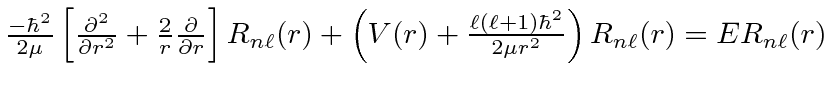
|
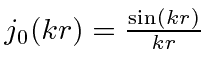 |
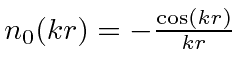
|
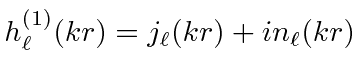
|
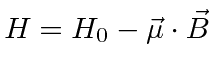 |
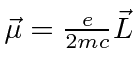
|
![\bgroup\color{black}$\int\limits_{-\infty}^\infty dx\; f(x)\; \delta(g(x))=\left[{1\over \vert{dg\over dx}\vert}f(x)\right]_{g(x)=0}$\egroup](img4633.png) |
|
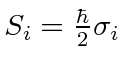
|
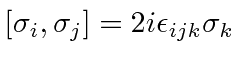
|
use
|
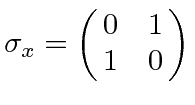
|
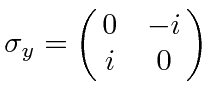
|
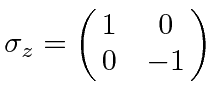 |
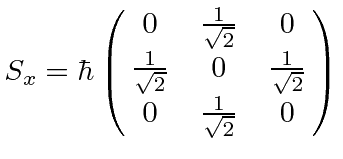
|
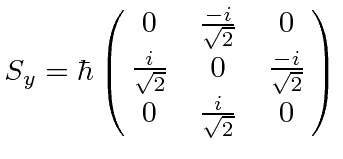
|
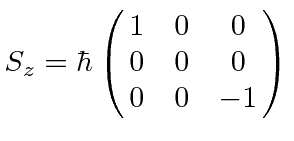 |
| GENERAL WAVE MECHANICS | ||
|
|
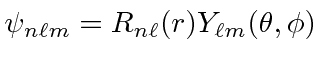 Ref.
Ref.
|
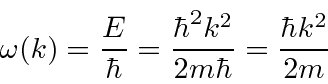 |
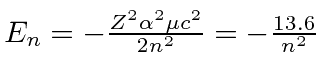 Ref.
Ref.
|
![\bgroup\color{black}$\Delta A\; \Delta B \geq \langle{i\over 2} [A,B]\rangle$\egroup](img4646.png) Ref.
Ref.
|
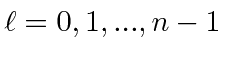 |
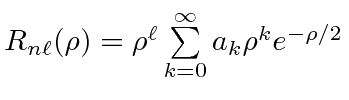 Ref.
Ref.
|
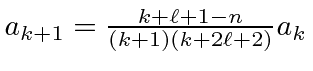 |
|
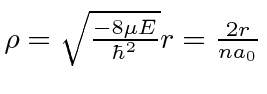 Ref.
Ref.
|
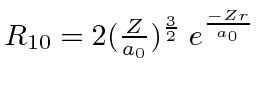 Ref.
Ref.
|
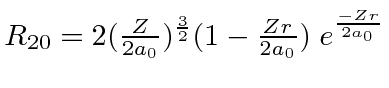 Ref.
Ref.
|
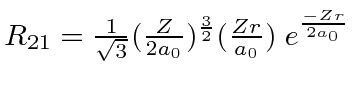
|
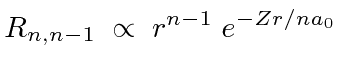 Ref.
Ref.
|
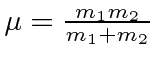 |
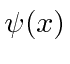 continuous continuous
|
|
|
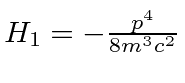 for for
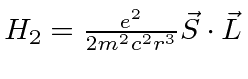 Ref.
Ref.
|
||
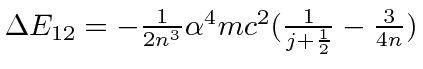
|
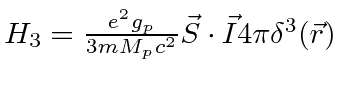 Ref.
Ref.
|
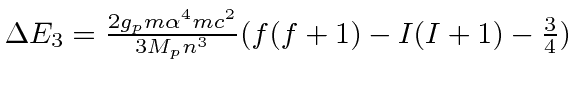 Ref.
Ref.
|
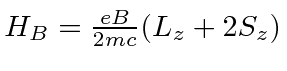
|
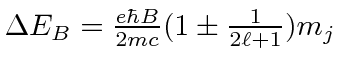
|
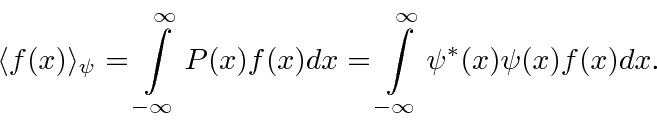 Ref.
Ref.
|
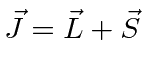 Ref.
Ref.
|
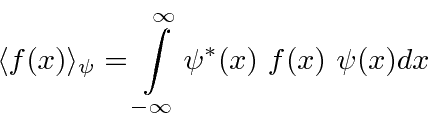 Ref.
Ref.
|
|
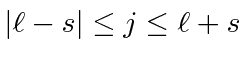
|
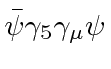 Ref.
Ref.
|
|
![\bgroup\color{black}$[p_x,x]={\hbar\over i}$\egroup](img3954.png) |
![\bgroup\color{black}$[L_x,L_y] = i \hbar L_z$\egroup](img4666.png) |
![\bgroup\color{black}$[L^2,L_z] = 0$\egroup](img4667.png) |
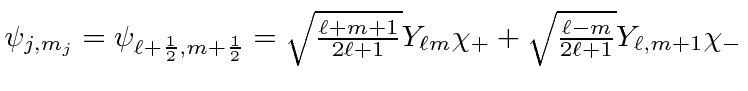 Ref.
Ref.
|
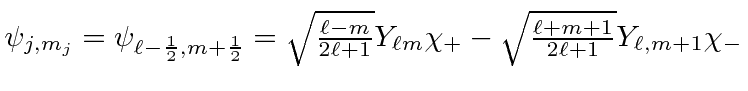 Ref.
Ref.
|
![\bgroup\color{black}${d\langle A\rangle \over dt}=
\langle {\partial A\over \partial t}\rangle +{i\over \hbar}\langle [H,A]\rangle $\egroup](img4670.png) Ref.
Ref.
|
| PERTURBATION THEORY AND RADIATIVE DECAYS | ||
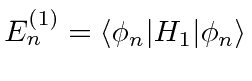 Ref.
Ref.
|
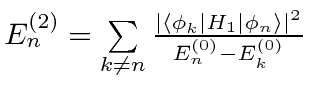
|
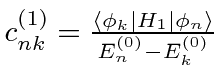 |
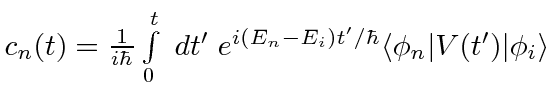 Ref.
Ref.
|
||
| Fermi's Golden Rule: |
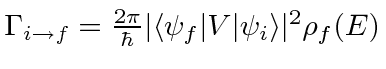 Ref.
Ref.
|
|
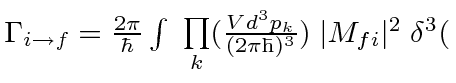 momentum conservation momentum conservation
|
||
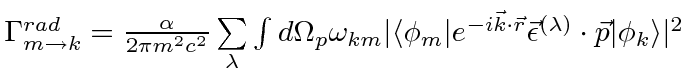 Ref.
Ref.
|
||
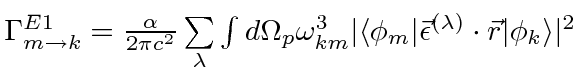 Ref.
Ref.
|
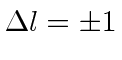 , ,
|
|
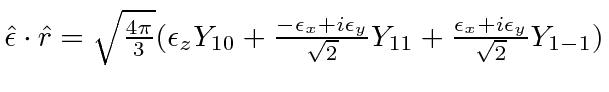
|
|
|
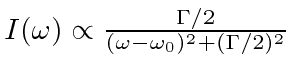 Ref.
Ref.
|
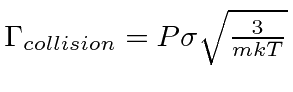
|
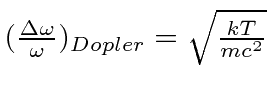
|
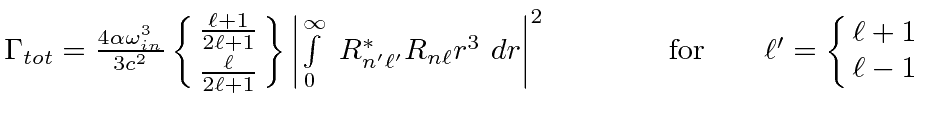 Ref.
Ref.
|
||
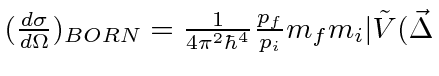
|
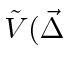
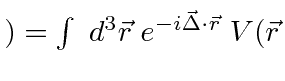
|
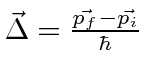 Ref.
Ref.
|
| ELECTRICITY AND MAGNETISM | ||
|
|
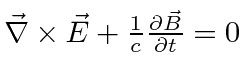
|
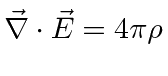 |
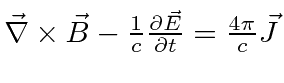
|
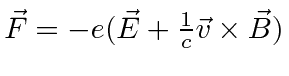
|
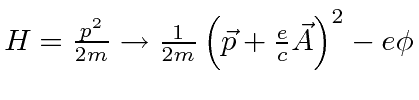 |
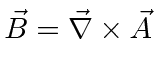
|
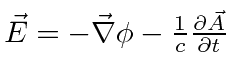
|
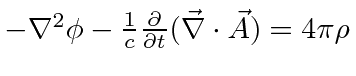 |
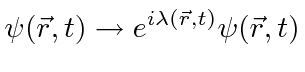
|
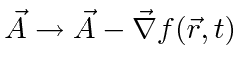
|
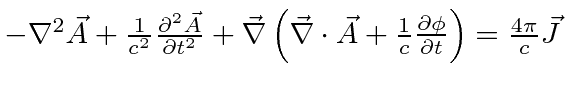 |
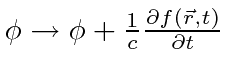
|
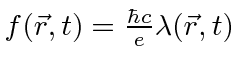 |
|
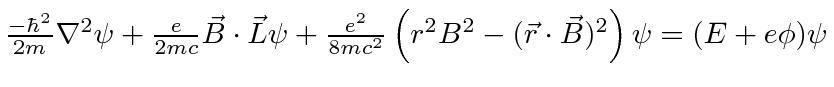 |
||
| ATOMS AND MOLECULES | ||
|
Hund: 1) max
|
2)max
|
3) min
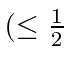 shell) else max shell) else max
|
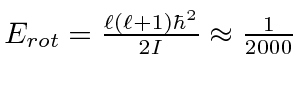 eV eV
|
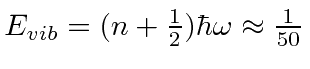 eV eV |
|
Branson 2008-12-22