Next: Parity of the Spherical Up: Angular Momentum Previous: Angular Momentum Algebra: Raising Contents
The angular momentum eigenstates are eigenstates of two operators.
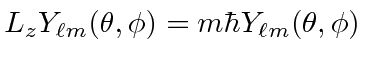
|
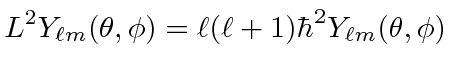 |
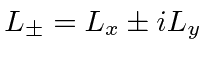 raise or lower
raise or lower
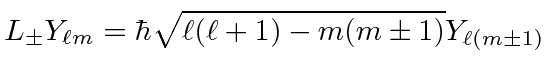 |
The differential operators take some work to derive.
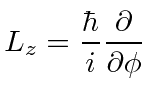
|
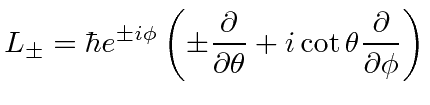 |
Its easy to find functions that give the eigenvalue of
![]() .
.
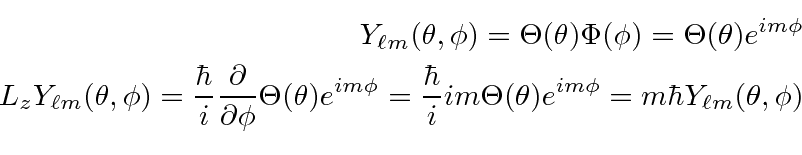
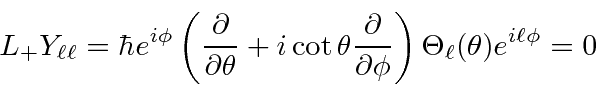
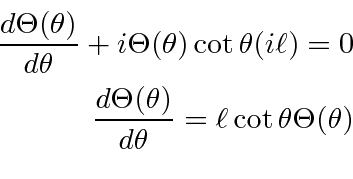
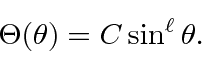
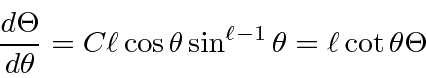
Here we should note that only the integer value of
![]() work for these solutions.
If we were to use half-integers, the wave functions would not be single valued,
for example at
work for these solutions.
If we were to use half-integers, the wave functions would not be single valued,
for example at
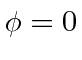 and
and
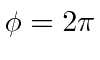 .
Even though the probability may be single valued, discontinuities in the amplitude would lead to infinities in the
Schrödinger equation.
We will find later that the half-integer angular momentum states are used for internal
angular momentum (spin), for which no
.
Even though the probability may be single valued, discontinuities in the amplitude would lead to infinities in the
Schrödinger equation.
We will find later that the half-integer angular momentum states are used for internal
angular momentum (spin), for which no
![]() or
or
![]() coordinates exist.
coordinates exist.
Therefore, the eigenstate ![]() is.
is.
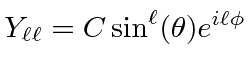 |
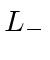 .
.
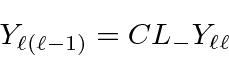
We call these eigenstates the Spherical Harmonics. The spherical harmonics are normalized.
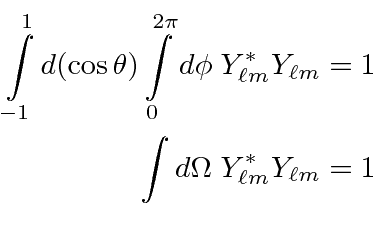
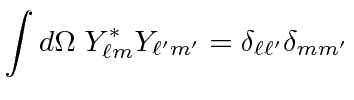 |
We will use the actual function in some problems.
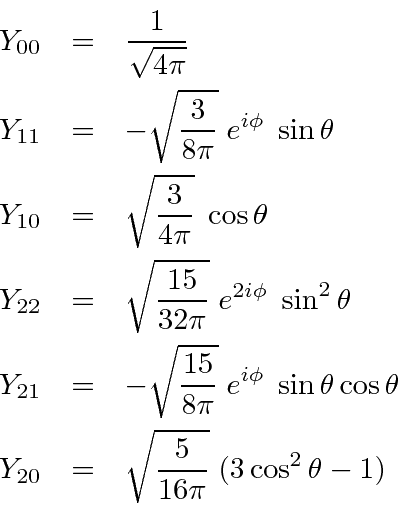
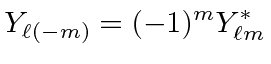 |
Any function of
![]() and
and
![]() can be expanded in the spherical harmonics.
can be expanded in the spherical harmonics.
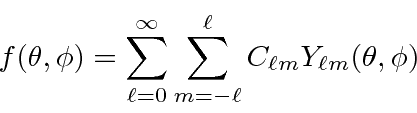
The spherical harmonics form a complete set.
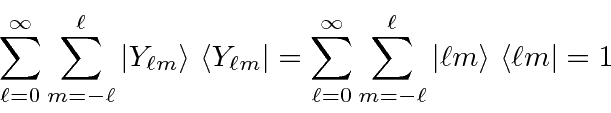
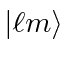 is sufficient to identify the state.
is sufficient to identify the state.
The spherical harmonics are related to the Legendre polynomials which are functions of
![]() .
.
![\begin{eqnarray*}
Y_{\ell 0}(\theta,\phi)&=&\left({2\ell+1\over 4\pi}\right)^{1...
...ell+m)!}\right]^{1\over 2}
P_\ell^m(\cos\theta)e^{im\phi} \\
\end{eqnarray*}](img1733.png)