Next: The Operators Up: Derivations and Computations Previous: Rewriting Using Contents
The transformation from spherical coordinates to Cartesian coordinate is.
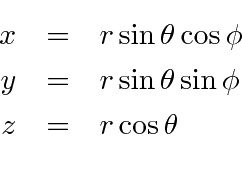
The transformation from Cartesian coordinates to spherical coordinates is.
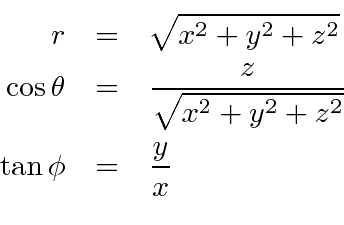
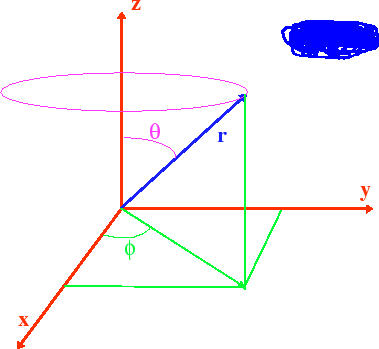
We now proceed to calculate the angular momentum operators in spherical coordinates.
The first step is to write the
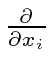 in spherical coordinates.
We use the chain rule and the above transformation from Cartesian to spherical.
We have used
in spherical coordinates.
We use the chain rule and the above transformation from Cartesian to spherical.
We have used
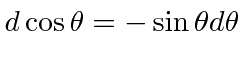 and
and
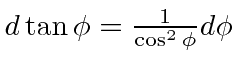 .
Ultimately all of these should be written in the sperical cooridnates but its convenient to use
.
Ultimately all of these should be written in the sperical cooridnates but its convenient to use
![]() for example in intermediate steps of the calculation.
for example in intermediate steps of the calculation.
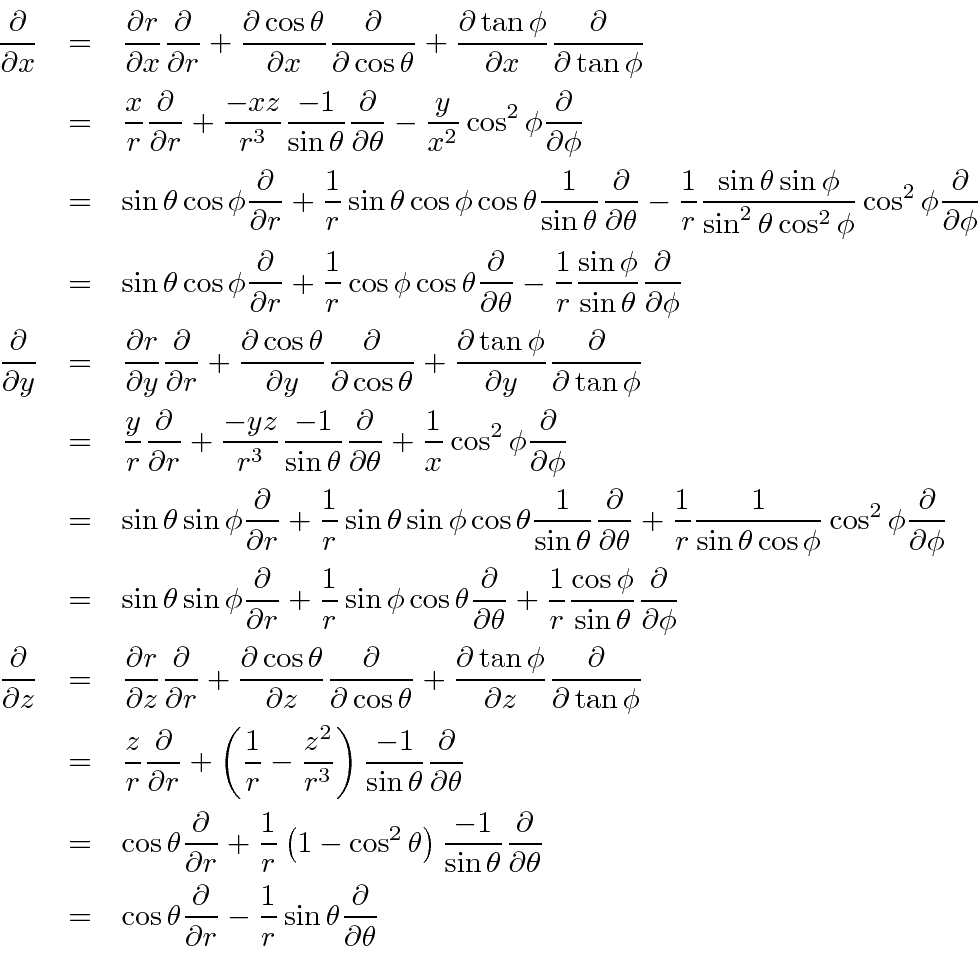
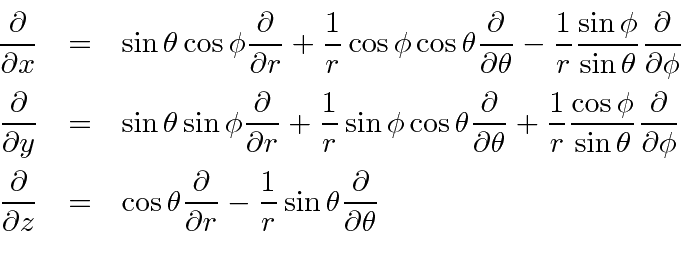
Now simply plug these into the angular momentum formulae.
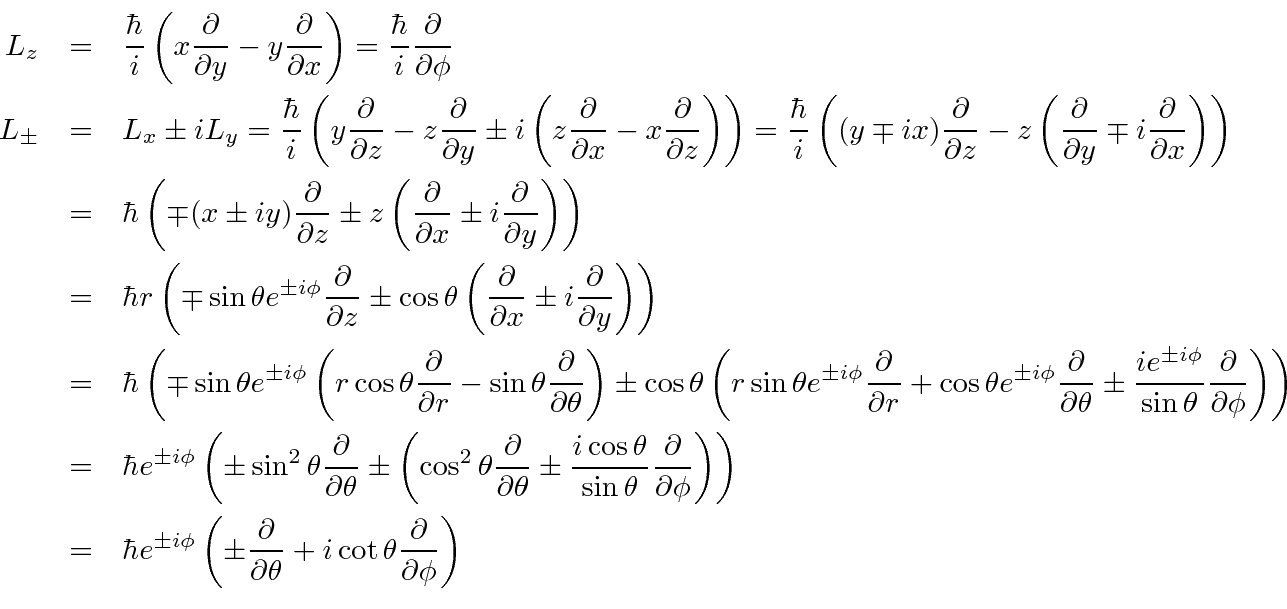
We will use these results to find the actual eigenfunctions of angular momentum.
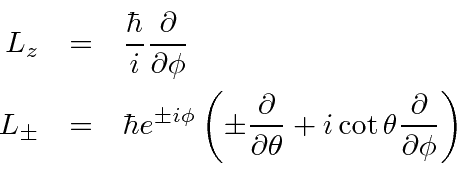
Jim Branson 2013-04-22