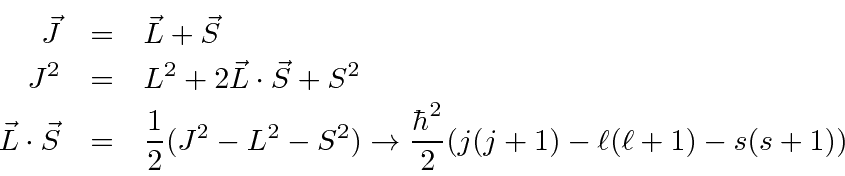The spin-orbit interaction (between magnetic dipoles) will play a role in the fine
structure of Hydrogen as well as in other problems.
It is a good example of the need for states of total angular momentum.
The additional term in the Hamiltonian is
If we define the total angular momentum 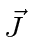 in the obvious way we can write
in the obvious way we can write
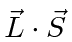 in terms of quantum numbers.
in terms of quantum numbers.
audio
Since our eigenstates of
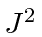 and
and
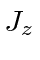 are also eigenstates of
are also eigenstates of
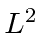 and
and
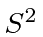 (but not
(but not
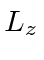 or
or
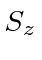 ),
these are ideal for computing the spin orbit interaction.
In fact, they are going to be the true energy eigenstates, as rotational symmetry tells
us they must.
),
these are ideal for computing the spin orbit interaction.
In fact, they are going to be the true energy eigenstates, as rotational symmetry tells
us they must.
Jim Branson
2013-04-22
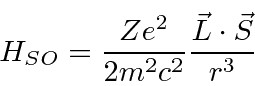
![]() in the obvious way we can write
in the obvious way we can write
![]() in terms of quantum numbers.
in terms of quantum numbers.