Next: The Photoelectric Effect Up: The Problems with Classical Previous: The Problems with Classical Contents
Radiation from a hot object is familiar to us. Objects around room temperature radiate mainly in the infrared as seen the the graph below.
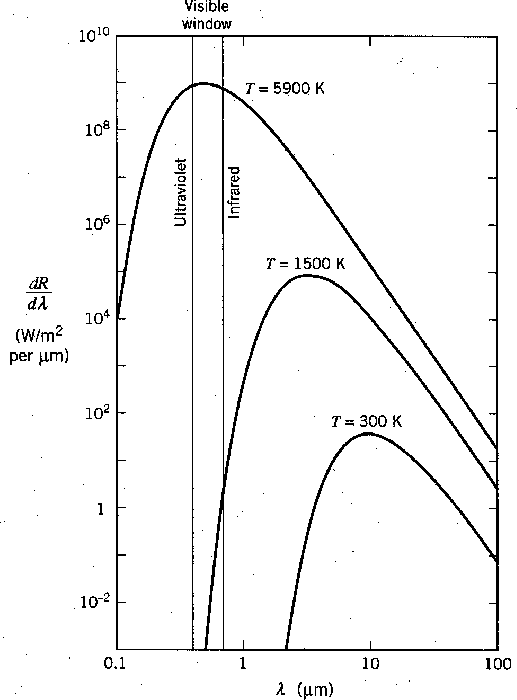
If we heat an object up to about 1500 degrees we will begin to see a dull red glow and we say the object is red hot. If we heat something up to about 5000 degrees, near the temperature of the sun's surface, it radiates well throughout the visible spectrum and we say it is white hot.
By considering plates in thermal equilibrium it can be shown that the emissive power over the absorption
coefficient must be the same as a function of wavelength, even for plates of different materials.
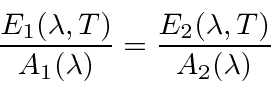

A black body is one that absorbs all radiation incident upon it.
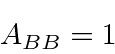
 , is universal and can be
derived from first principles.
, is universal and can be
derived from first principles.
A good example of a black body is a cavity with a small hole in it. Any light incident upon the hole goes into the cavity and is essentially never reflected out since it would have to undergo a very large number of reflections off walls of the cavity. If we make the walls absorptive (perhaps by painting them black), the cavity makes a perfect black body.
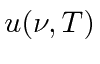 ,
and the black body emissive power of a black body
which simply comes from an analysis of how much radiation, traveling at the speed of light,
will flow out of a hole in the cavity in one second.
,
and the black body emissive power of a black body
which simply comes from an analysis of how much radiation, traveling at the speed of light,
will flow out of a hole in the cavity in one second.
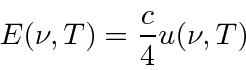
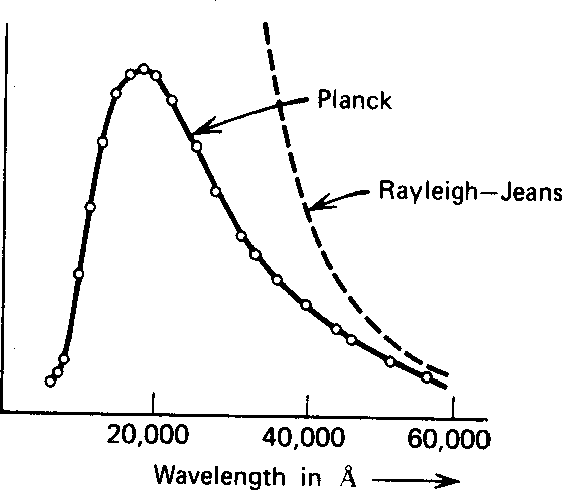
Rayleigh and Jeans
calculated
t he energy density (in EM waves) inside a cavity
and hence the emission spectrum of a black body.
Their calculation was based on simple EM theory and equipartition.
It not only did not agree with data;
it said that all energy would be instantly radiated away in high frequency EM radiation.
This was called the ultraviolet catastrophe.
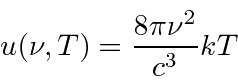
Plank found a formula that fit the data well at both long and short wavelength.
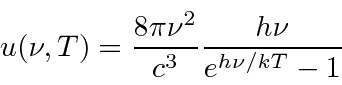
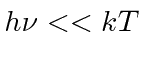 but goes to zero at large
but goes to zero at large
It is interesting to note that classical EM waves would suck all the thermal energy out of matter,
making the universe a very cold place for us.
The figure below compares the two calculations to some data at
![]() degrees.
(It is also surprising that the start of the Quantum revolution came from Black Body radiation.)
degrees.
(It is also surprising that the start of the Quantum revolution came from Black Body radiation.)
So the emissive power per unit area is
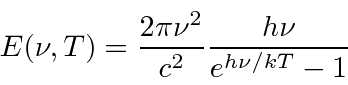
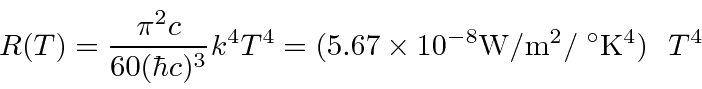
* Example:
What is the temperature at the solar surface? Use both the the intensity of radiation on earth
and that the spectrum peaks about 500 nm to get answers.*
* Example:
The cosmic microwave background is black body radiation with a temperature of 2.7 degrees.
For what frequency (and what wavelength) does the intensity peak?*
Jim Branson 2013-04-22