Next: Examples Up: Derivations and Computations Previous: Eigenfunctions of Hermitian Operators Contents
We can use the Schrödinger Equation to show that the first derivative of the wave function should be continuous, unless the potential is infinite at the boundary.
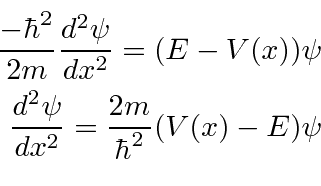
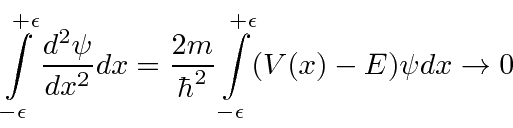
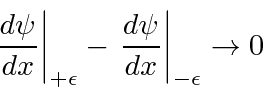
Infinite potentials are unphysical but often handy.
The delta function potential is very handy, so we will derive a special continuity equation for it.
Assume
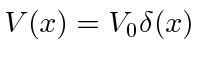 . Integrating the Schrödinger Equation, we get
. Integrating the Schrödinger Equation, we get
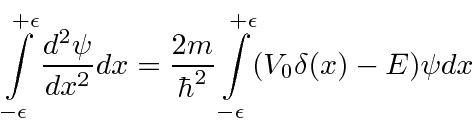
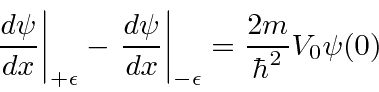
Jim Branson 2013-04-22