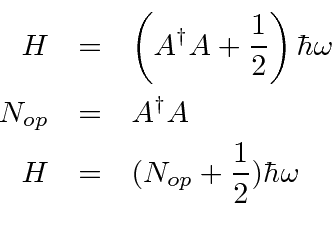Next: Raising and Lowering Constants Up: Harmonic Oscillator Solution using Previous: Commutators of , and Contents
We have computed the commutators
![\begin{eqnarray*}[H,A]&=&-\hbar\omega A \\
{[H,A^\dagger]}&=&\hbar\omega A^\dagger \\
\end{eqnarray*}](img1429.png)
Apply
![\bgroup\color{black}$[H,A]$\egroup](img182.png) to the energy eigenfunction
to the energy eigenfunction
![]() .
.
![\begin{eqnarray*}[H,A]u_n=-\hbar\omega Au_n \\
HAu_n-AHu_n=-\hbar\omega Au_n \\...
...(Au_n)=-\hbar\omega Au_n \\
H(Au_n)=(E_n-\hbar\omega)(Au_n) \\
\end{eqnarray*}](img1444.png)
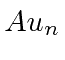 is an eigenfunction of
is an eigenfunction of
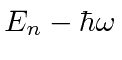 .
Therefore,
.
Therefore,
Now, apply
![\bgroup\color{black}$[H,A^\dagger]$\egroup](img1447.png) to the energy eigenfunction
to the energy eigenfunction
![]() .
.
![\begin{eqnarray*}[H,A^\dagger]u_n=\hbar\omega A^\dagger u_n \\
HA^\dagger u_n-A...
...r u_n) \\
H(A^\dagger u_n)=(E_n+\hbar\omega)(A^\dagger u_n) \\
\end{eqnarray*}](img1448.png)
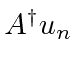 is an eigenfunction of
is an eigenfunction of
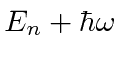 .
.
We cannot keep lowering the energy because the HO energy cannot go below zero.
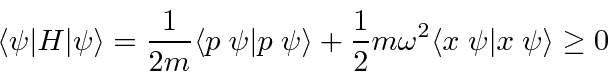
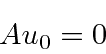
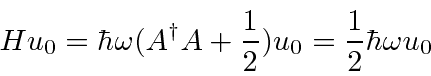
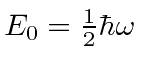 and the states in general have energies
and the states in general have energies
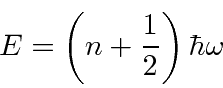
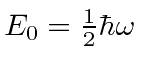 can stop the lowering
so the only energies allowed are
can stop the lowering
so the only energies allowed are
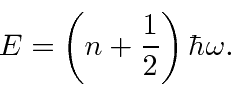
It is interesting to note that we have a number operator for
![]()