Next: Unitary Operators Up: Operators in a Vector Previous: Review of Operators Contents
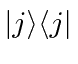 and Completeness
and Completeness
Now we move on a little with our understanding of operators.
A ket vector followed by a bra vector is an example of an operator.
For example the operator which projects a vector onto the ![]() eigenstate is
eigenstate is
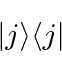
The sum of the projection operators is 1, if we sum over a complete set of states, like the eigenstates of a Hermitian operator.
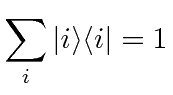 |
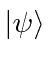 above.
above.
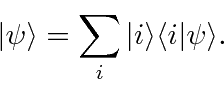
The same is true for definite momentum states.
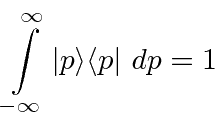 |
We can form a projection operator into a subspace.
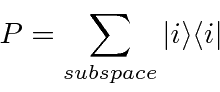
Jim Branson 2013-04-22