Next: Homework Problems Up: Derivations and Computations Previous: The Darwin Term Contents
We compute the energy change due to a weak magnetic field using first order Perturbation Theory.
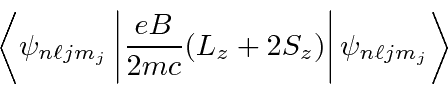
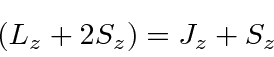
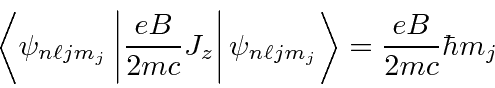
The
![]() is harder since we are not in eigenstates of that one.
We need
is harder since we are not in eigenstates of that one.
We need
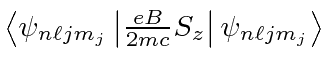 ,
but we don't know how
,
but we don't know how
![]() acts on these.
So, we must write
acts on these.
So, we must write
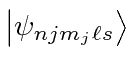 in terms of
in terms of
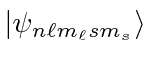 .
.
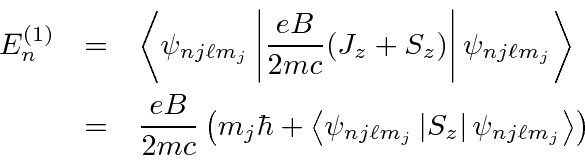
We already know how to write in terms of these states of definite
![]() and
and
![]() .
.
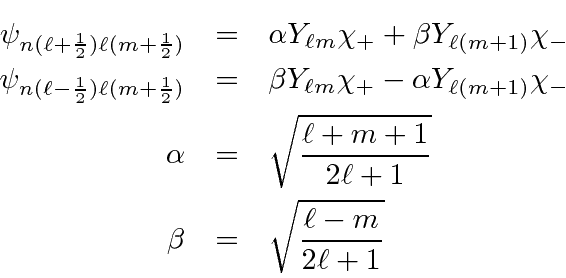
Let's do the
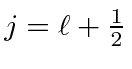 state first.
state first.
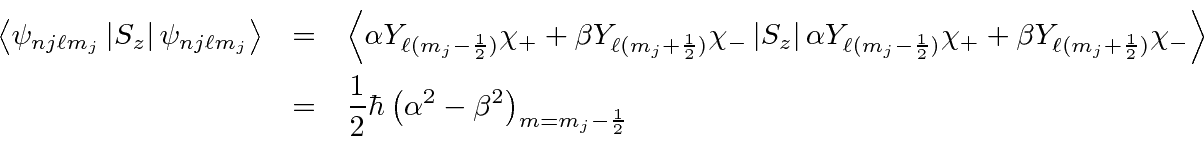
For
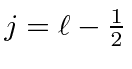 ,
,
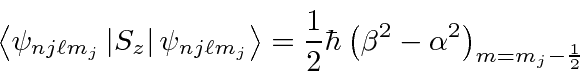
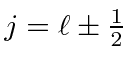 .
.
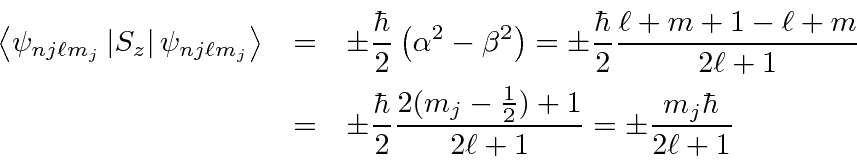
So adding this to the (easier) part above, we have
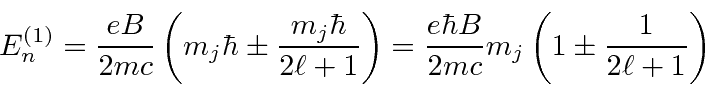
for
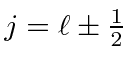 .
.
In summary then, we
rewrite the fine structure shift.
![\begin{displaymath}\bgroup\color{black}\Delta E=-{1\over 2}mc^2\left(Z\alpha\rig...
...n^3}}\left[ {1\over{j+{1\over 2}}} -{3\over{4n}}\right].\egroup\end{displaymath}](img3134.png)
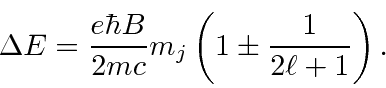
Jim Branson 2013-04-22