Next: Position Space and Momentum Up: Wave Packets Previous: Two Examples of Localized Contents
The wave packets we tried above satisfy an
uncertainty principle which is a property of waves.
That is
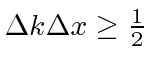 .
.
For the ``square'' packet the full width in
![]() is
is
![]() .
The width in
.
The width in
![]() is a little hard to define, but, lets use the first node in the probability
found at
is a little hard to define, but, lets use the first node in the probability
found at
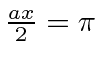 or
or
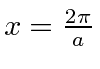 .
So the width is twice this or
.
So the width is twice this or
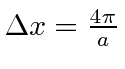 .
This gives us
.
This gives us
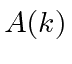 , the width of
, the width of
 changes to keep the uncertainty product constant.
changes to keep the uncertainty product constant.
For the Gaussian wave packet, we can rigorously read the RMS width of the probability distribution as was done at the end of the section on the Fourier Transform of a Gaussian.
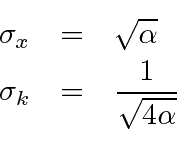
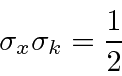
If we translate into momentum
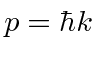 , then
, then
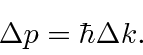
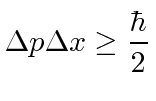 |
If we try to localize a particle to a very small region of space, its momentum becomes uncertain. If we try to make a particle with a definite momentum, its probability distribution spreads out over space.
Jim Branson 2013-04-22