Hyperfine Correction in Hydrogen

We start from the magnetic moment of the nucleus

$$\bgroup\color{black}\vec{\mu}={Zeg_N\over 2M_Nc}\vec{I}.\egroup$$

Now we use the classical vector potential from a point dipole (see (green) Jackson page 147)

$$\bgroup\color{black}\vec{A}(\vec{r})=-(\vec{\mu}\times\vec{\nabla}){1\over r}.\egroup$$

We compute the field from this.

$$\bgroup\color{black}\vec{B}=\vec{\nabla}\times\vec{A}\egroup$$

$$\bgroup\color{black}B_k={\partial\over \partial x_i}A_j\epsil... ...r \partial x_n}(-\epsilon_{mnj}\epsilon_{ikj}){1\over r}\egroup$$

$$\bgroup\color{black}=-\mu_m{\partial\over \partial x_i}{\part... ...artial x_i}{\partial\over \partial x_k}\right){1\over r}\egroup$$

$$\bgroup\color{black}\vec{B}=-\left(\vec{\mu}\nabla^2{1\over r}-\vec{\nabla}(\vec{\mu}\cdot\vec{\nabla}){1\over r}\right)\egroup$$

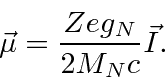
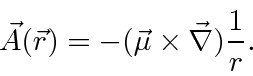
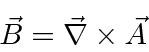
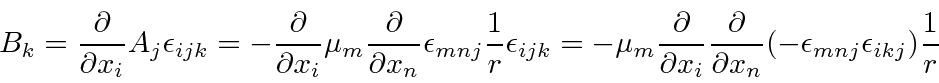
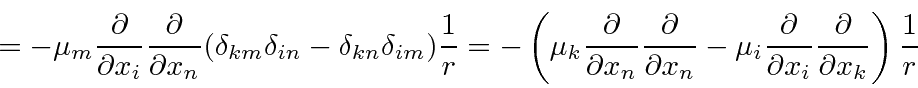
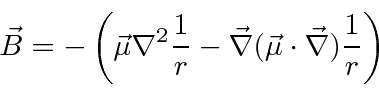
Then we compute the energy shift in first order perturbation theory for s states.

$$\bgroup\color{black}\Delta E = \left<{e\over{m_ec}}\vec S\cdo... ...}}{\partial\over{\partial x_j}}{1\over r}\right>\right) \egroup$$

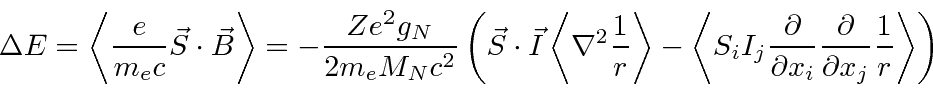
The second term can be simplified because of the spherical symmetry of s states. (Basically the derivative with respect to x is odd in x so when the integral is done, only the terms where 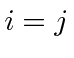$i=j$ are nonzero).

$$\bgroup\color{black}\int d^3r \vert\phi_{n00}(\vec{r})\vert... ... d^3r \vert\phi_{n00}(\vec{r})\vert^2\nabla^2{1\over r}\egroup$$

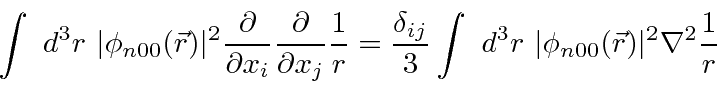
So we have

$$\bgroup\color{black}\Delta E = -{2\over 3}{Ze^2g_N\over{2 m_eM_Nc^2}} \vec S\cdot\vec I\left<\nabla^2{1\over r}\right>. \egroup$$

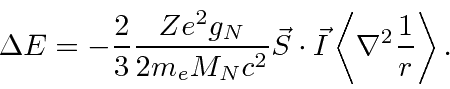
Now working out the $\nabla^2$ term in spherical coordinates,

$$\bgroup\color{black}\left({\partial^2\over{\partial r^2}}+{2\... ...= {2\over {r^3}}+{2\over r}\left({-1\over{r^2}}\right)=0\egroup$$

we find that it is zero everywhere but we must be careful at $r=0$.

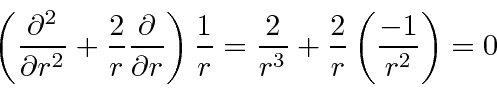
To find the effect at $r=0$ we will integrate.

$$\bgroup\color{black} \int\limits^\varepsilon_{r=0}\vec\nabla^... ...vec{dS} = \int {\partial\over{\partial r}}{1\over r} dS \egroup$$

$$\bgroup\color{black} =\int\limits^\varepsilon_{r=0} {-1\over{... ... = (4\pi\varepsilon^2)({-1\over\varepsilon^2}) = -4\pi \egroup$$

So the integral is nonzero for any region including the origin, which implies

$$\bgroup\color{black}\left(\nabla^2{1\over r}\right)=-4\pi\delta^3(\vec{r}).\egroup$$

We can now evaluate the expectation value.

$$\bgroup\color{black}\Delta E = -{2\over 3}{Ze^2g_N\over{2 m_e... ...^2}} \vec S\cdot\vec I (-4\pi\vert\phi_{n00}(0)\vert^2) \egroup$$

$$\bgroup\color{black}4\pi\vert\phi_{n00}(0)\vert^2=\vert R_{n0... ...ert^2={4\over n^3}\left(Z\alpha m_ec\over\hbar\right)^3 \egroup$$

$$\bgroup\color{black}\Delta E ={2\over 3}{Ze^2g_N\over{2 m_eM_... ...ec I {4\over n^3}\left(Z\alpha m_ec\over\hbar\right)^3 \egroup$$

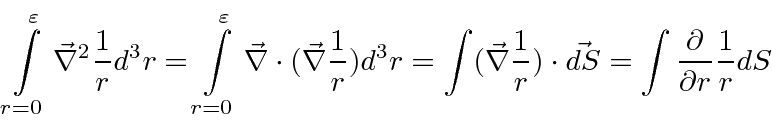
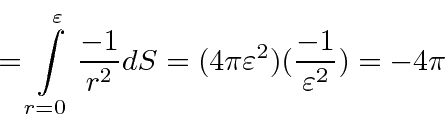
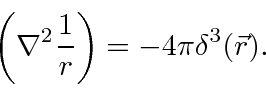
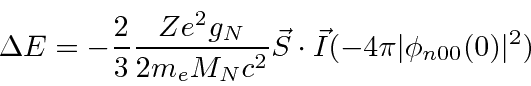
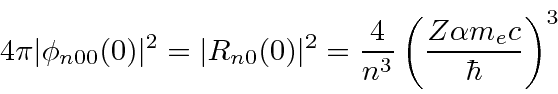
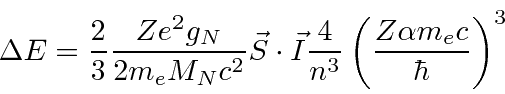
Simply writing the $e^2$ in terms of $\alpha$ and regrouping, we get

$$\bgroup\color{black} \Delta E = {4\over 3} (Z\alpha)^4 \left(... ... g_N {1\over{n^3}} {\vec{S}\cdot\vec{I}\over{\hbar^2}}. \egroup$$

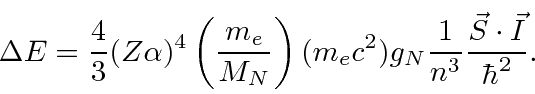
We will sometimes group the constants such that

$$\bgroup\color{black} \Delta E \equiv {{\cal A}\over\hbar^2} \vec{S}\cdot\vec{I}.\egroup$$

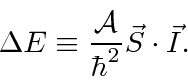
(The textbook has numerous mistakes in this section.)