Next: Black Body Radiation * Up: Quantum Physics 130 Previous: The Dirac Equation Contents
By the late nineteenth century the laws of physics were based on Mechanics and the law of Gravitation from Newton, Maxwell's equations describing Electricity and Magnetism, and on Statistical Mechanics describing the state of large collection of matter. These laws of physics described nature very well under most conditions, however, some measurements of the late 19th and early 20th century could not be understood. The problems with classical physics led to the development of Quantum Mechanics and Special Relativity.
Some of the problems leading to the development of Quantum Mechanics are listed here.
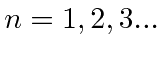 , that gave the right result for hydrogen, but turned out to be wrong since
the ground state of hydrogen has zero angular momentum.
It took a full understanding of Quantum Mechanics to explain the atomic energy spectra.
, that gave the right result for hydrogen, but turned out to be wrong since
the ground state of hydrogen has zero angular momentum.
It took a full understanding of Quantum Mechanics to explain the atomic energy spectra.
Quantum Mechanics incorporates a wave-particle duality and explains all of the above phenomena. In doing so, Quantum Mechanics changes our understanding of nature in fundamental ways. While the classical laws of physics are deterministic, QM is probabilistic. We can only predict the probability that a particle will be found in some region of space.
Electromagnetic waves like light are made up of particles we call photons.
Einstein, based on Plank's formula,
hypothesized that the particles of light had energy proportional to their frequency.
The new idea of Quantum Mechanics is that every particle's probability (as a function of position and time) is equal to the square of a probability amplitude function and that these probability amplitudes obey a wave equation. This is much like the case in electromagnetism where the energy density goes like the square of the field and hence the photon probability density goes like the square of the field, yet the field is made up of waves. So probability amplitudes are like the fields we know from electromagnetism in many ways.
DeBroglie assumed
![]() for photons and other particles and used Lorentz invariance (from special relativity)
to derive the
wavelength for particles like electrons.
for photons and other particles and used Lorentz invariance (from special relativity)
to derive the
wavelength for particles like electrons.
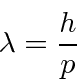
* Example:
Assume the photon is a particle with the standard deBroglie wavelength.
Use kinematics to derive the wavelength of the scattered photon as a function of angle for Compton Scattering.*
Gasiorowicz Chapter 1
Rohlf Chapters 3,6
Griffiths does not really cover this.
Cohen-Tannoudji et al. Chapter