Next: Derivations and Computations Up: Atomic Spectra * Previous: Atomic Spectra * Contents
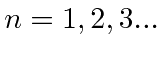 .
This is natural since
.
This is natural since
Balance of forces for circular orbits.
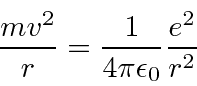
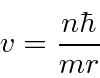
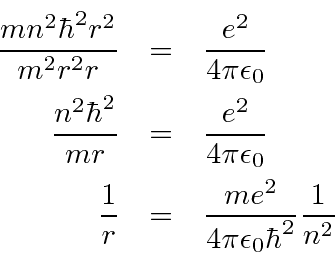
Now we just want to plug
![]() and
and
![]() into the energy formula.
We write the Hydrogen potential in terms of the
fine structure constant
into the energy formula.
We write the Hydrogen potential in terms of the
fine structure constant
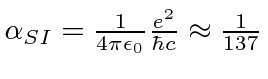 .
.
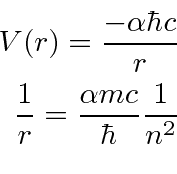
We now compute the energy levels.
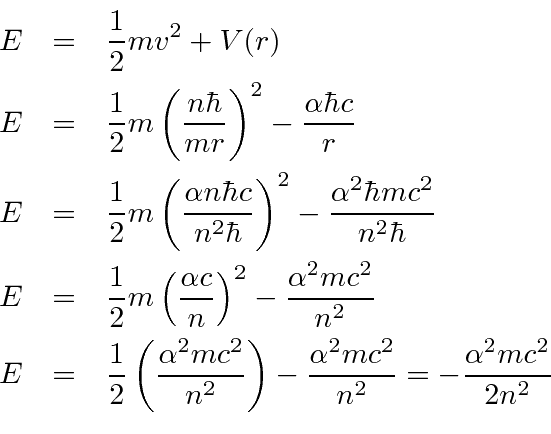
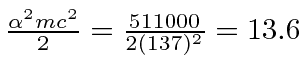 eV.
Bohr's formula gives the
right Hydrogen energy spectrum.
eV.
Bohr's formula gives the
right Hydrogen energy spectrum.
We can also compute the ground state radius of the Bohr orbit.
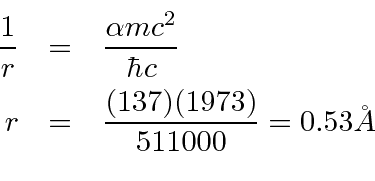
Although angular momentum is quantized in units of
![]() ,
the ground state of Hydrogen has zero angular momentum.
This would put Bohr's electron in the nucleus.
,
the ground state of Hydrogen has zero angular momentum.
This would put Bohr's electron in the nucleus.
Bohr fit the data, with some element of truth, but his model is WRONG.
Jim Branson 2013-04-22