Next: Black Body Radiation from Up: Examples Previous: Examples Contents
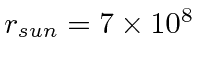 m,
m,
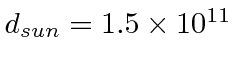 m)
m)
First we compute the power radiated per unit area on the solar surface.
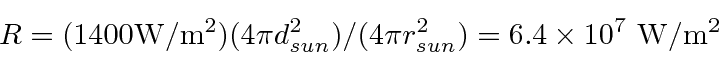
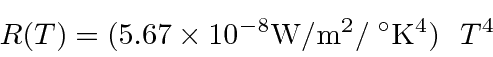
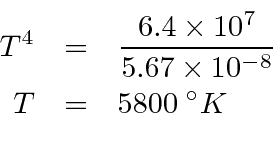
Lets assume that
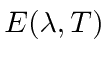 peaks at 500 nm as one of the graphs shows.
We need to transform
peaks at 500 nm as one of the graphs shows.
We need to transform
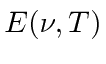 .
Remember
.
Remember
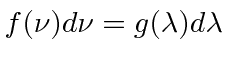 for distribution functions.
for distribution functions.
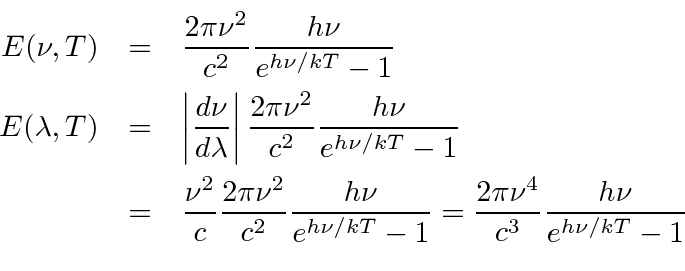
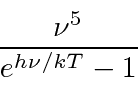
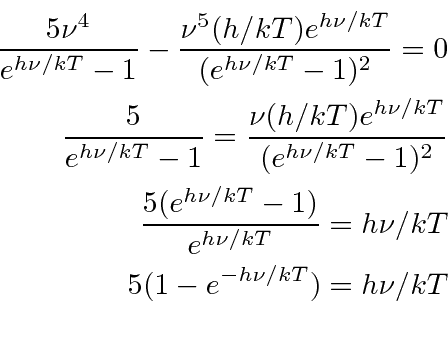
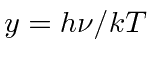 and solve the equation
and solve the equation
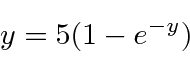
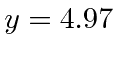 implying
implying
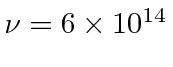 .
.
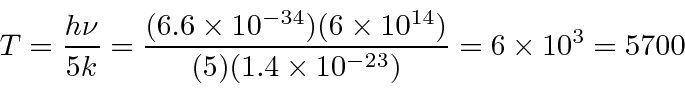
Jim Branson 2013-04-22