Next: Compton Scattering * Up: Examples Previous: The Solar Temperature * Contents
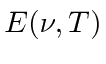 is a maximum for the 2.7 degree cosmic background radiation.
Find the wavelength
is a maximum for the 2.7 degree cosmic background radiation.
Find the wavelength
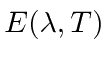 is a maximum.
is a maximum.
The cosmic background radiation was produced when the universe was much hotter than it is now.
Most of the atoms in the universe were ionized and photons interacted often with the ions or free electrons.
As the universe cooled so that neutral atoms formed, the photons decoupled from matter and just propagated
through space.
We see these photons today as the background radiation.
Because the universe is expanding, the radiation has been red shifted down to a much lower temperature.
We observe about 2.7 degrees.
The background radiation is very uniform but we are beginning to observe non-uniformities at the
![]() level.
level.
From the previous problem, we can say that the peak
![]() occurs when
occurs when
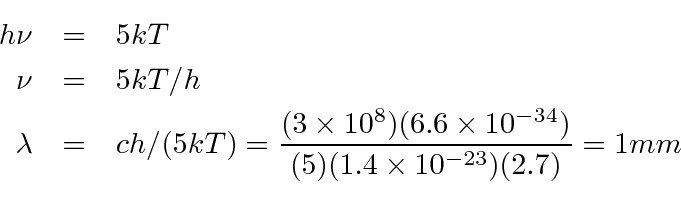
Similarly the peak in
![]() occurs when
occurs when
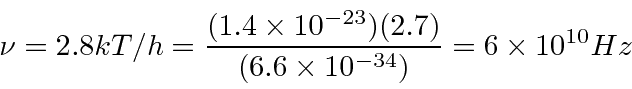
Jim Branson 2013-04-22