Next: The Problems with Classical Up: Course Summary Previous: The Dirac Equation Contents
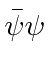 is a scalar and that we can form a scalar
from the dot product of two 4-vectors as in the Lagrangian below.
The Lagrangian cannot depend explicitly on the coordinates.
is a scalar and that we can form a scalar
from the dot product of two 4-vectors as in the Lagrangian below.
The Lagrangian cannot depend explicitly on the coordinates.

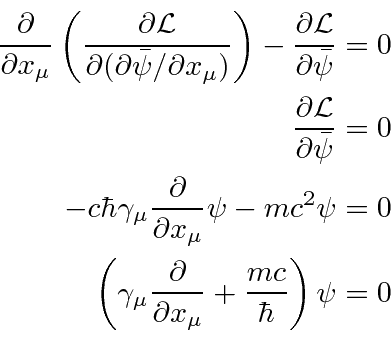
The Hamiltonian density may be derived from the Lagrangian in the standard way and the total Hamiltonian
computed by integrating over space.
Note that the Hamiltonian density is the same as the Hamiltonian derived from the Dirac equation directly.
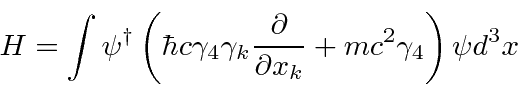
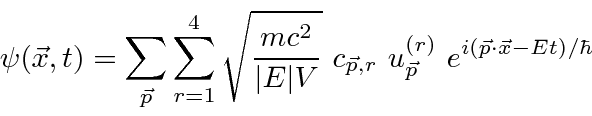
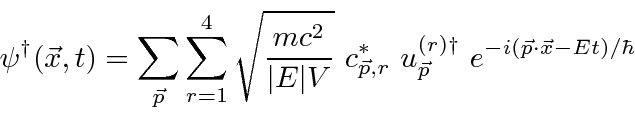
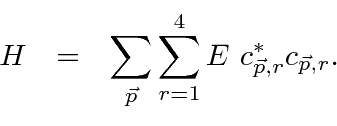
By analogy with electromagnetism, we can replace the Fourier coefficients for the Dirac plane waves by operators.
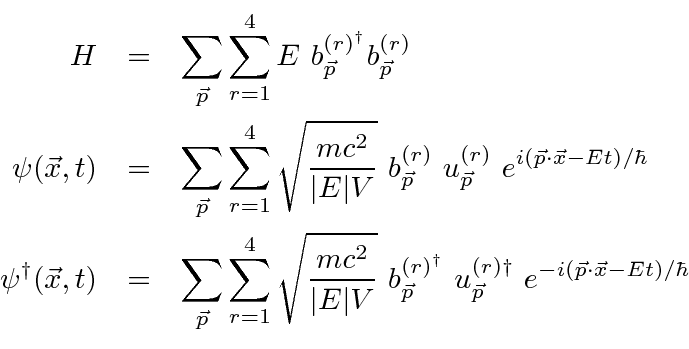
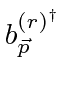 and
and
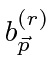 satisfy anticommutation relations.
satisfy anticommutation relations.
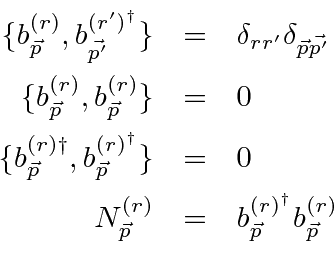
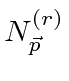 is the occupation number operator.
The anti-commutation relations constrain the occupation number to be 1 or 0.
is the occupation number operator.
The anti-commutation relations constrain the occupation number to be 1 or 0.
The Dirac field and Hamiltonian can now be rewritten in terms of electron and positron fields for which the energy is always positive by replacing the operator to annihilate a ``negative energy state'' with an operator to create a positron state with the right momentum and spin.
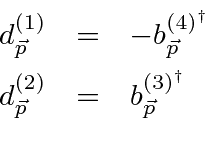
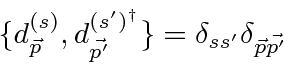
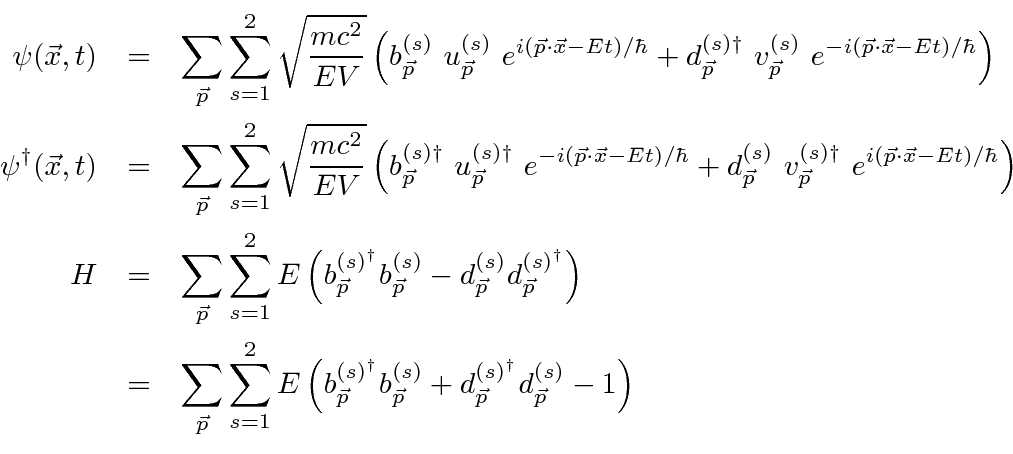
There is an (infinite) constant energy, similar but of opposite sign to the one for the quantized EM field, which we must add to make the vacuum state have zero energy. Note that, had we used commuting operators (Bose-Einstein) instead of anti-commuting, there would have been no lowest energy ground state so this Energy subtraction would not have been possible. Fermi-Dirac statistics are required for particles satisfying the Dirac equation.
Since the operators creating fermion states anti-commute,
fermion states must be antisymmetric under interchange.
Assume
![]() and
and
![]() are the creation and annihilation operators for fermions and that they anti-commute.
are the creation and annihilation operators for fermions and that they anti-commute.
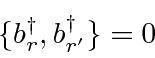
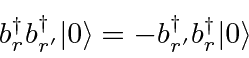
Note that the spinors satisfy the following slightly different equations.
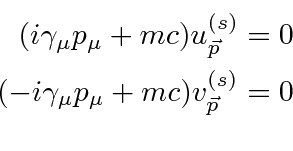
Jim Branson 2013-04-22