The DeBroglie Wavelength

The Lorentz transformation had been postulated for ElectroMagnetic waves before Einstein developed Special Relativity. The EM waves were entirely consistent with Relativity. For example, the phase of an EM wave at some point is the same as at the Lorentz transformed point.

DeBroglie applied this Lorentz invariance requirement on the phase of matter waves to determine what the wavelength must be. Its easy for us to derive the wavelength using 4-vectors. Position and time form one 4-vector.

$$\bgroup\color{black}x^\mu=(ct,\vec{x})\egroup$$

Energy and momentum form another.

$$\bgroup\color{black}p^\mu=(E,\vec{p}c)\egroup$$

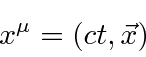
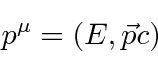
Recall that Lorentz vectors must be transformed but Lorentz scalars are automatically invariant under transformations. For example the scalar formed by dotting the 4-momentum into itself is

$$\bgroup\color{black}p^\mu p_\mu=-E^2+p^2c^2=-m^2c^4.\egroup$$

The mass of a particle is clearly Lorentz invariant.

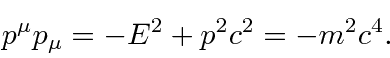
To compute the wavelength for our matter waves, lets use the scalar

$$\bgroup\color{black}p^\mu x_\mu/c=-Et+\vec{p}\cdot\vec{x}\egroup$$

Its already easy to see that the phase in a wave like

$$\bgroup\color{black}e^{i(\vec{p}\cdot\vec{x}-Et)/\hbar}\egroup$$

is Lorentz invariant.

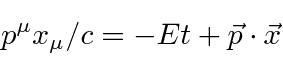
To read off the wavelength, lets pick off the part of the expression that corresponds to $e^{2\pi i(x/\lambda-\nu t)}$. We see that 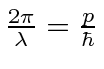${2\pi\over\lambda}={p\over\hbar}$ and therefore the DeBroglie wavelength is.

$$\lambda={2\pi\hbar\over p}={h\over p}$$

DeBroglie derived this result in 1923.

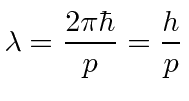We can also read off the frequency $\nu$.

$$\bgroup\color{black}\nu={E\over 2\pi\hbar}=E/h\egroup$$

This was in some sense the input to our calculation.

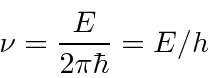
The deBroglie wavelength will be our primary physics input for the development of Quantum Mechanics. Its not that this work was the most significant, but, this wavelength summarizes most of what happened before 1923.