Next: Wave Particle Duality (Thought Up: The DeBroglie Wavelength Previous: The DeBroglie Wavelength Contents
The whole problem of computing a deBroglie wavelength is to convert from kinetic energy to momentum.
If you always want to be correct without any need for thinking,
use the
relativistically correct formula for the kinetic energy
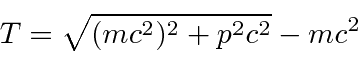
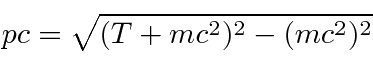
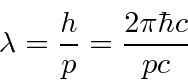
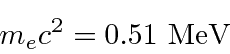
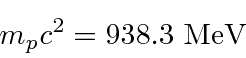
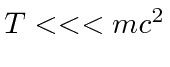 , make sure the precision of your calculator sufficient
or use the non-relativistic method below.)
, make sure the precision of your calculator sufficient
or use the non-relativistic method below.)
If you know that the particle is super-relativistic, so that
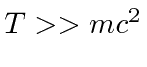 ,
then just use
,
then just use
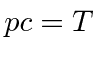 and life is easy.
and life is easy.
If you know that the particle is highly non-relativistic,
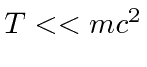 , then you can use
, then you can use
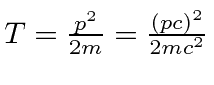 giving
giving
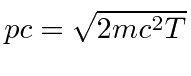 .
.
So, for example, compute the wavelength of a 100 eV electron.
This is non-relativistic since 100 eV « 510000 eV.
So
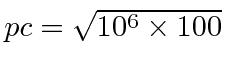 eV or 10000 eV.
eV or 10000 eV.
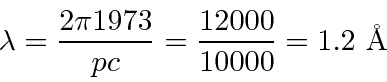
Jim Branson 2013-04-22