More Fun with Operators

We find the time development operator by solving the equation $i\hbar{\partial\psi\over\partial t}=H\psi$.

$$\bgroup\color{black}\psi(t)=e^{-iHt/\hbar}\psi(t=0)\egroup$$

This implies that $e^{-iHt/\hbar}$ is the time development operator. In some cases we can calculate the actual operator from the power series for the exponential.

$$\bgroup\color{black}e^{-iHt/\hbar}=\sum\limits_{n=0}^\infty{(-iHt/\hbar)^n\over n!}\egroup$$

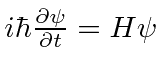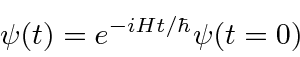
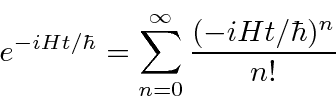
We have been working in what is called the Schrödinger picture in which the wavefunctions (or states) develop with time. There is the alternate Heisenberg picture in which the operators develop with time while the states do not change. For example, if we wish to compute the expectation value of the operator $B$ as a function of time in the usual Schrödinger picture, we get

$$\bgroup\color{black}\langle\psi(t)\vert B\vert\psi(t)\rangle=... ...0)\vert e^{iHt/\hbar}Be^{-iHt/\hbar}\vert\psi(0)\rangle.\egroup$$

In the Heisenberg picture the operator $B(t)=e^{iHt/\hbar}Be^{-iHt/\hbar}$.

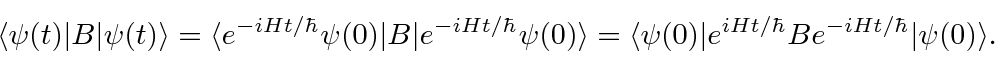
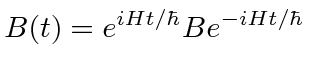We use operator methods to compute the uncertainty relationship between non-commuting variables

$$\bgroup\color{black}(\Delta A)(\Delta B)\geq{i\over 2}\langle[A,B]\rangle\egroup$$

which gives the result we deduced from wave packets for $p$ and $x$.

Again we use operator methods to calculate the time derivative of an expectation value.

$$\bgroup\color{black}{d\over dt}\langle\psi\vert A\vert\psi\ra... ...rtial A\over\partial t}\right\vert\psi\right\rangle_\psi\egroup$$

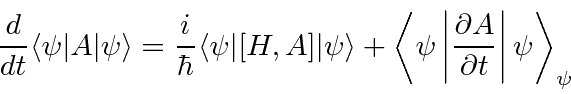
(Most operators we use don't have explicit time dependence so the second term is usually zero.) This again shows the importance of the Hamiltonian operator for time development. We can use this to show that in Quantum mechanics the expectation values for $p$ and $x$ behave as we would expect from Newtonian mechanics (Ehrenfest Theorem).

$$\bgroup\color{black}{d\langle x\rangle\over dt}={i\over\hbar}... ...2\over 2m},x]\rangle=\left\langle{p\over m}\right\rangle\egroup$$

$$\bgroup\color{black}{d\langle p\rangle\over dt}={i\over\hbar}... ...\right\rangle=-\left\langle{dV(x)\over dx} \right\rangle\egroup$$

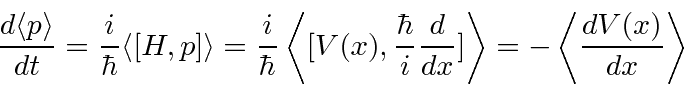
Any operator $A$ that commutes with the Hamiltonian has a time independent expectation value. The energy eigenfunctions can also be (simultaneous) eigenfunctions of the commuting operator $A$. It is usually a symmetry of the $H$ that leads to a commuting operator and hence an additional constant of the motion.