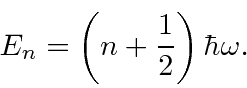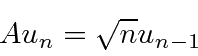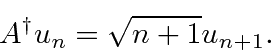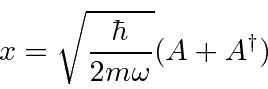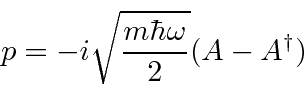We can solve the
harmonic oscillator problem using operator methods.
We write the Hamiltonian in terms of the operator
.
We compute the commutators
If we apply the the commutator
![\bgroup\color{black}$[H,A]$\egroup](img182.png) to the eigenfunction
to the eigenfunction
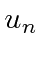 ,
we get
,
we get
![\bgroup\color{black}$[H,A]u_n=-\hbar\omega Au_n$\egroup](img184.png) which rearranges to the eigenvalue equation
which rearranges to the eigenvalue equation
This says that
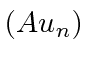 is an eigenfunction of
is an eigenfunction of
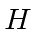 with eigenvalue
with eigenvalue
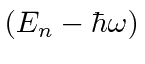 so it lowers the energy by
so it lowers the energy by
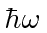 .
Since the energy must be positive for this Hamiltonian, the lowering must stop somewhere,
at the ground state, where we will have
.
Since the energy must be positive for this Hamiltonian, the lowering must stop somewhere,
at the ground state, where we will have
This allows us to compute the ground state energy like this
showing that the ground state energy is
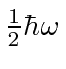 .
Similarly,
.
Similarly,
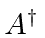 raises the energy by
raises the energy by
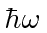 .
We can travel up and down the energy ladder using
.
We can travel up and down the energy ladder using
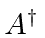 and
and
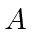 ,
always in steps of
,
always in steps of
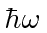 .
The energy eigenvalues are therefore
.
The energy eigenvalues are therefore
A little more computation shows that
and that
These formulas are useful for all kinds of computations within the important
harmonic oscillator system.
Both
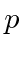 and
and
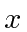 can be written in terms of
can be written in terms of
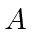 and
and
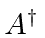 .
.
Jim Branson
2013-04-22
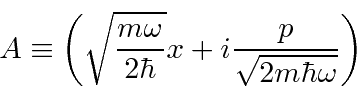
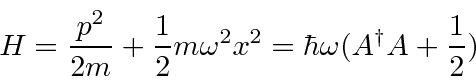
![\begin{displaymath}\bgroup\color{black}[A,A^\dagger]={i\over 2\hbar}(-[x,p]+[p,x])=1 \egroup\end{displaymath}](img179.png)
![\begin{displaymath}\bgroup\color{black}[H,A]=\hbar\omega[A^\dagger A,A]=\hbar\omega[A^\dagger,A]A=-\hbar\omega A\egroup\end{displaymath}](img180.png)
![\begin{displaymath}\bgroup\color{black}[H,A^\dagger]=\hbar\omega[A^\dagger A,A^\...
...\hbar\omega A^\dagger[A,A^\dagger]=\hbar\omega A^\dagger\egroup\end{displaymath}](img181.png)
![\bgroup\color{black}$[H,A]$\egroup](img182.png) to the eigenfunction
to the eigenfunction
![\bgroup\color{black}$[H,A]u_n=-\hbar\omega Au_n$\egroup](img184.png) which rearranges to the eigenvalue equation
which rearranges to the eigenvalue equation
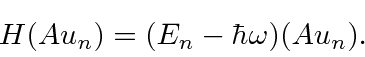
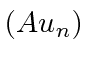 is an eigenfunction of
is an eigenfunction of
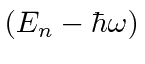 so it lowers the energy by
so it lowers the energy by
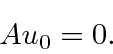
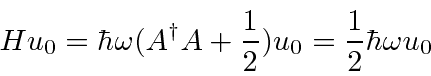
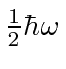 .
Similarly,
.
Similarly,