Next: Harmonic Oscillator Solution with Up: Course Summary Previous: The Harmonic Oscillator in Contents
The
delta function potential
is a very useful one to make simple models of molecules and solids.
First we solve the problem with one attractive delta function
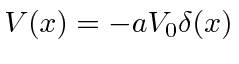 .
Since the bound state has negative energy, the solutions that are normalizable
are
.
Since the bound state has negative energy, the solutions that are normalizable
are
![]() for
for
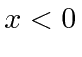 and
and
![]() for
for
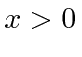 .
Making
.
Making
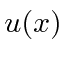 continuous and its first derivative have a discontinuity
computed from the Schr
continuous and its first derivative have a discontinuity
computed from the Schr
![]() dinger equation at
dinger equation at
![]() ,
gives us exactly one bound state with
,
gives us exactly one bound state with
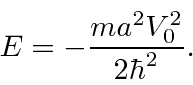
Next we use two delta functions to
model a molecule,
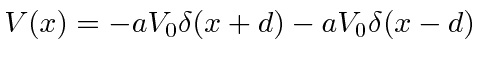 .
Solving this problem by matching wave functions at the boundaries at
.
Solving this problem by matching wave functions at the boundaries at
![]() ,
we find again transcendental equations for two bound state energies.
The ground state energy is more negative than that for one delta function,
indicating that the molecule would be bound.
A look at the wavefunction shows that the 2 delta function state can lower
the kinetic energy compared to the state for one delta function,
by reducing the curvature of the wavefunction.
The excited state has more curvature than the atomic state so we would not
expect molecular binding in that state.
,
we find again transcendental equations for two bound state energies.
The ground state energy is more negative than that for one delta function,
indicating that the molecule would be bound.
A look at the wavefunction shows that the 2 delta function state can lower
the kinetic energy compared to the state for one delta function,
by reducing the curvature of the wavefunction.
The excited state has more curvature than the atomic state so we would not
expect molecular binding in that state.
Our final 1D potential, is a
model of a solid.
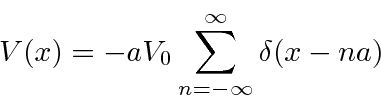
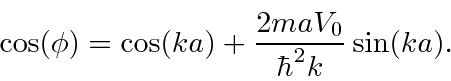
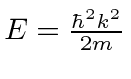 which do not have solutions.
There are also bands of energies with solutions.
These energy bands are seen in crystals (like Si).
which do not have solutions.
There are also bands of energies with solutions.
These energy bands are seen in crystals (like Si).
Jim Branson 2013-04-22