Next: The Quantum Rotor Up: One Dimensional Potentials Previous: The Delta Function Model Contents
The Kronig-Penny model of a solid crystal contains an
infinite array of repulsive delta functions.
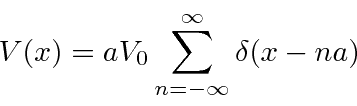
This potential has a new symmetry,
that a translation by the lattice spacing ![]() leaves the problem unchanged.
The probability distributions must therefore have this symmetry
leaves the problem unchanged.
The probability distributions must therefore have this symmetry
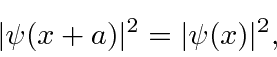
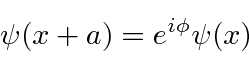
The general solution in the region
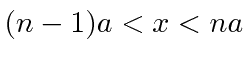 is
is
![\begin{displaymath}\bgroup\color{black} \psi_n(x)=A_n\sin(k[x-na])+B_n\cos(k[x-na]) \egroup\end{displaymath}](img1303.png)
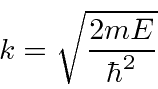
By matching the boundary conditions and requiring that the probability be periodic, we
derive a constraint on
![]() similar to the quantized energies for bound states.
similar to the quantized energies for bound states.
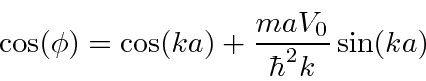
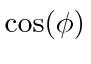 can only take on values between -1 and 1, there are
allowed bands of
can only take on values between -1 and 1, there are
allowed bands of
The graph below shows
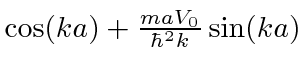 as a function of
as a function of
![]() .
If this is not between -1 and 1, there is no solution, that value of
.
If this is not between -1 and 1, there is no solution, that value of
![]() and the corresponding energy are not allowed.
and the corresponding energy are not allowed.
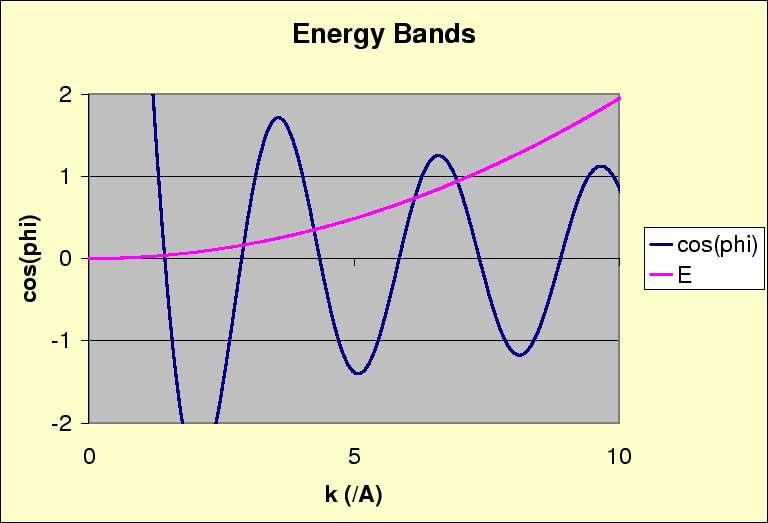
This energy band phenomenon is found in solids. Solids with partially filled bands are conductors. Solids with filled bands are insulators. Semiconductors have a small number of charge carriers (or holes) in a band.
Jim Branson 2013-04-22