Next: Derivations and Computations Up: One Dimensional Potentials Previous: The Delta Function Model Contents
It is useful to simply investigate angular momentum with just one free rotation angle. This might be the quantum plane propeller. We will do a good job of this in 3 dimensions later.
Lets assume we have a mass ![]() constrained to move in a circle of radius
constrained to move in a circle of radius ![]() .
Assume the motion in the circle is free, so there is no potential.
The kinetic energy is
.
Assume the motion in the circle is free, so there is no potential.
The kinetic energy is
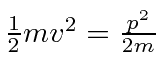 for
for
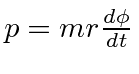 .
.
If we measure distance around the circle, then
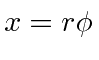 and the one problem we have is that once I go
completely around the circle, I am back to
and the one problem we have is that once I go
completely around the circle, I am back to
![]() .
Lets just go ahead and write our wavefunction.
.
Lets just go ahead and write our wavefunction.
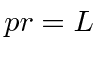 .
Our wave is
.
Our wave is
This must be single valued so we need to require that
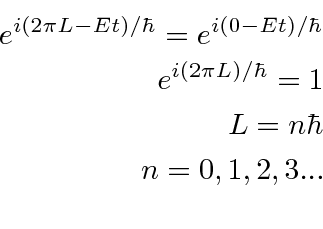
This will prove to be true for 3 dimensions too, however, the 3 components of angular momentum do not commute with each other, leading to all kinds of fun.
Jim Branson 2013-04-22