1D Model of a Crystal Derivation *

We are working with the periodic potential

$$\bgroup\color{black} V(x)=aV_0\sum\limits_{n=-\infty}^\infty \delta(x-na) .\egroup$$

Our states have positive energy. This potential has the symmetry that a translation by the lattice spacing $a$ leaves the problem unchanged. The probability distributions must therefore have this symmetry

$$\bgroup\color{black} \vert\psi(x+a)\vert^2=\vert\psi(x)\vert^2 ,\egroup$$

which means that the wave function differs by a phase at most.

$$\bgroup\color{black} \psi(x+a)=e^{i\phi}\psi(x) \egroup$$

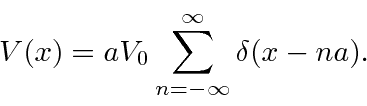
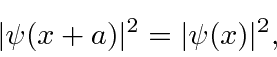
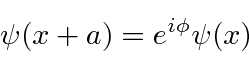
The general solution in the region 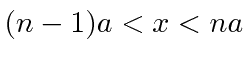$(n-1)a<x<na$ is

$$\bgroup\color{black} \psi_n(x)=A_n\sin(k[x-na])+B_n\cos(k[x-na]) \egroup$$

$$\bgroup\color{black} k=\sqrt{2mE\over\hbar^2} \egroup$$

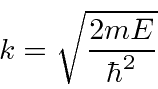
Now lets look at the boundary conditions at $x=na$. Continuity of the wave function gives

$$\begin{eqnarray*} \psi_n(na)&=&\psi_{n+1}(na) \\ A_n\sin(0)+B_n\cos(0)&=&A_{n+1... ...1}\cos(ka) \\ B_{n+1}&=&{B_n+A_{n+1}\sin(ka)\over\cos(ka)} .\\ \end{eqnarray*}$$

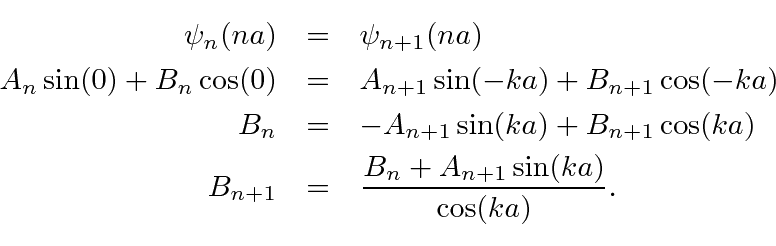
The discontinuity in the first derivative is

$$\begin{eqnarray*} \left.{d\psi_{n+1}\over dx}\right\vert _{na} -\left.{d\psi_{n... ...A_{n+1}\cos(ka)+B_{n+1}\sin(ka)-A_n]={2maV_0\over\hbar^2}B_n \\ \end{eqnarray*}$$

Substituting 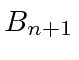$B_{n+1}$ from the first equation

$$\begin{eqnarray*} k[A_{n+1}\cos(ka)+[B_n+A_{n+1}\sin(ka)]\tan(ka)-A_n]={2maV_0\o... ...+1}={2maV_0\over\hbar^2k}B_n\cos(ka)-B_n\sin(ka)+A_n\cos(ka) \\ \end{eqnarray*}$$

Plugging this equation for 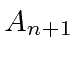$A_{n+1}$ back into the equation above for 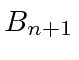$B_{n+1}$ we get

$$\begin{eqnarray*} B_{n+1}&=&{B_n+A_{n+1}\sin(ka)\over\cos(ka)} \\ B_{n+1}&=&{B_... ...&=&{2maV_0\over\hbar^2k}B_n\sin(ka)+B_n\cos(ka)+A_n\sin(ka) .\\ \end{eqnarray*}$$

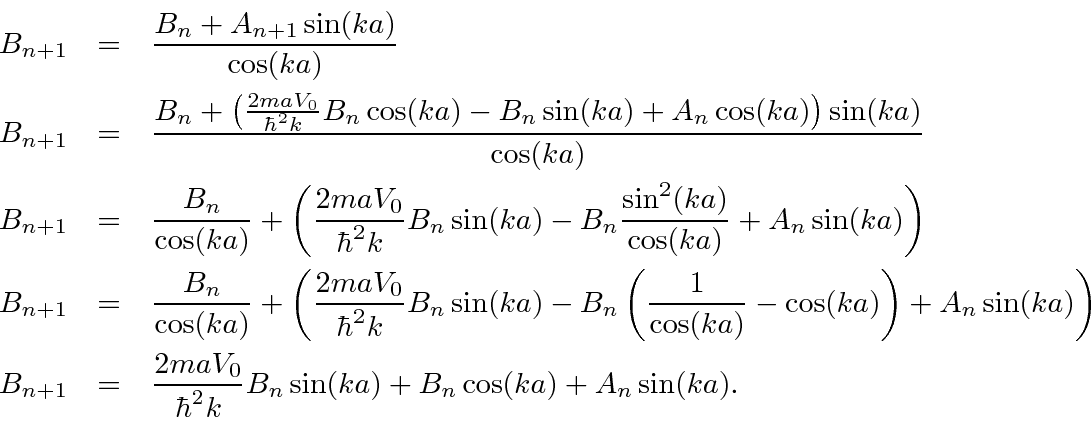
We now have two pairs of equations for the 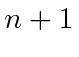$n+1$ coefficients in terms of the $n$ coefficients.

$$\begin{eqnarray*} A_{n+1}&=&{2maV_0\over\hbar^2k}B_n\cos(ka)-B_n\sin(ka)+A_n\cos... ...in(ka) \\ A_{n+1}&=&e^{i\phi}A_n \\ B_{n+1}&=&e^{i\phi}B_n \\ \end{eqnarray*}$$

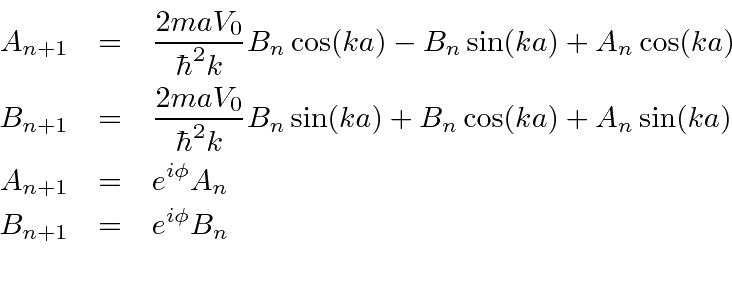
Using the second pair of equations to eliminate the 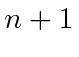$n+1$ coefficients, we have

$$\begin{eqnarray*} (e^{i\phi}-\cos(ka))A_n=\left({2maV_0\over\hbar^2k}\cos(ka)-\s... ...cos(ka)-{2maV_0\over\hbar^2k}\sin(ka)\right)B_n=\sin(ka)A_n .\\ \end{eqnarray*}$$

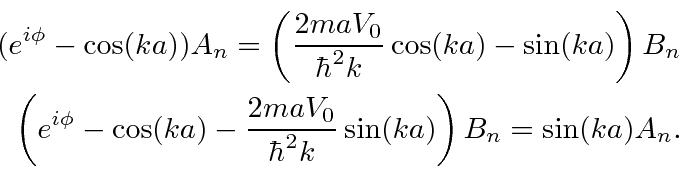
Now we can eliminate all the coefficients.

$$\begin{eqnarray*} (e^{i\phi}-\cos(ka))(e^{i\phi}-\cos(ka)-{2maV_0\over\hbar^2k}\... ...phi}\left({2maV_0\over\hbar^2k}\sin(ka)+2\cos(ka)\right)+1=0 \\ \end{eqnarray*}$$

Multiply by $e^{-i\phi}$.

$$\begin{eqnarray*} e^{i\phi}+e^{-i\phi}-\left({2maV_0\over\hbar^2k}\sin(ka)+2\cos... ...ight)=0 \\ \cos(\phi)=\cos(ka)+{maV_0\over\hbar^2k}\sin(ka) \\ \end{eqnarray*}$$

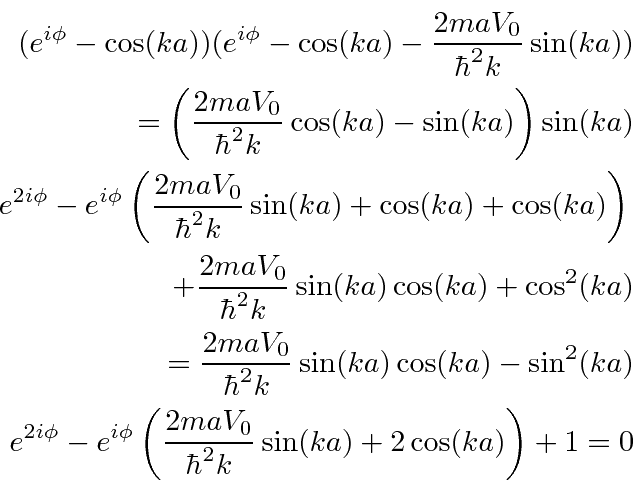
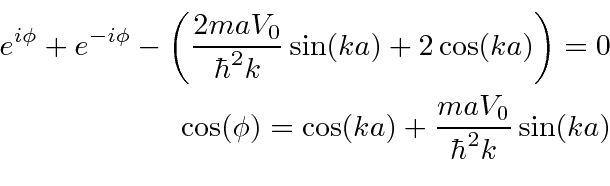
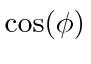This relation puts constraints on $k$, like the constraints that give us quantized energies for bound states. Since $\cos(\phi)$ can only take on values between -1 and 1, there are allowed bands of $k$ and gaps between those bands.