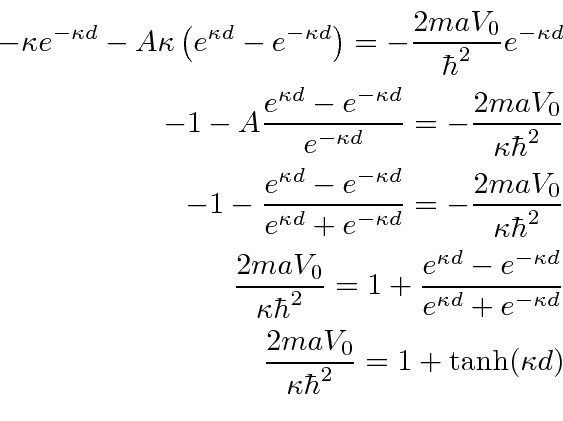1D Model of a Molecule Derivation *
Since the solution is designed to be symmetric about
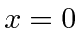 , the boundary conditions at
, the boundary conditions at
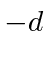 are the same as at
are the same as at
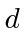 .
The boundary conditions determine the constant
.
The boundary conditions determine the constant
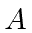 and constrain
and constrain
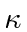 .
.
Continuity of
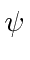 gives.
gives.
The discontinuity in the first derivative of
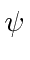 at
at
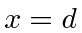 is
is
We'll need to study this transcendental equation to see what the allowed energies are.
Jim Branson
2013-04-22
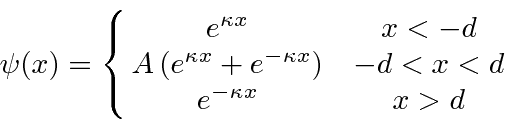
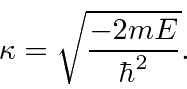
![]() gives.
gives.
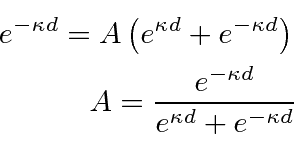
![]() at
at
![]() is
is