Next: 1D Model of a Up: Derivations and Computations Previous: Bound States of a Contents
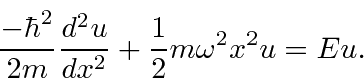
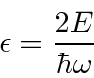
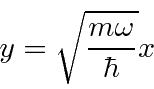
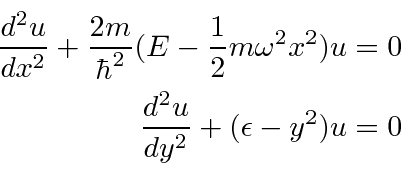
(Its probably easiest to just check the above equation by substituting as below.
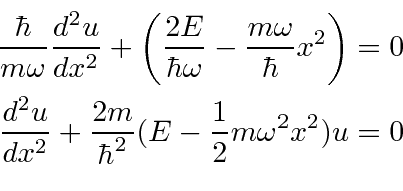
Now we want to find the solution for
 .
.
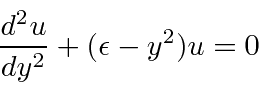
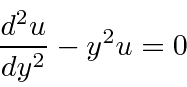
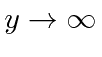 so we can write our general solution as
so we can write our general solution as
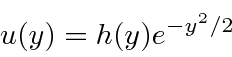
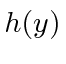 is a polynomial.
is a polynomial.
Take the differential equation
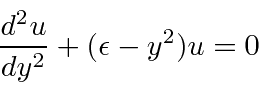
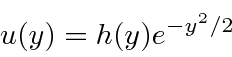
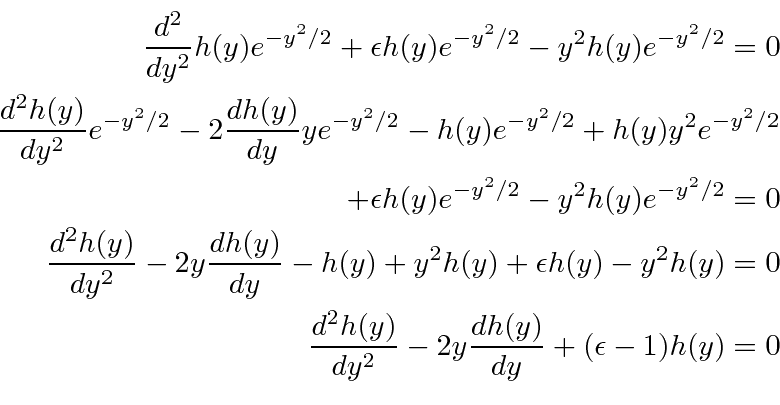
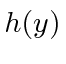 .
.
Write
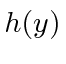 as a sum of terms.
as a sum of terms.
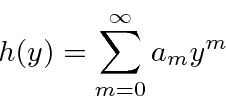
![\begin{displaymath}\bgroup\color{black}\sum\limits_{m=0}^\infty[ a_m (m)(m-1)y^{m-2}-2a_m(m)y^m+(\epsilon-1)a_my^m ]=0\egroup\end{displaymath}](img1355.png)
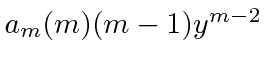 down two steps in the sum.
It will now show up as
down two steps in the sum.
It will now show up as
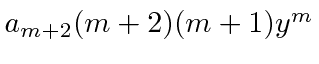 .
.
![\begin{displaymath}\bgroup\color{black} \sum\limits_{m=0}^\infty[ a_{m+2} (m+2)(m+1)-2a_m(m)+(\epsilon-1)a_m ]y^m=0\egroup\end{displaymath}](img1359.png)
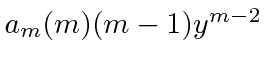 is zero for
is zero for
For the sum to be zero for all
![]() , each coefficient of
, each coefficient of
![]() must be zero.
must be zero.
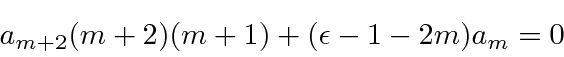
Solve for
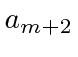
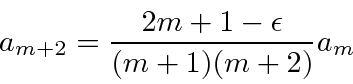
But, lets see what we have. For large
![]() ,
,
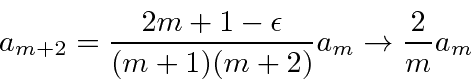
The series for
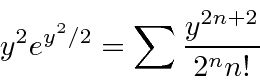
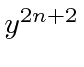 equal to
equal to
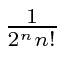 and
the coefficient of
and
the coefficient of
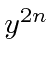 equal to
equal to
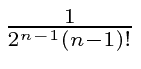 .
If
.
If
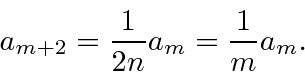
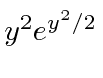 and our overall solution will not
be normalizable.
(Remember
and our overall solution will not
be normalizable.
(Remember
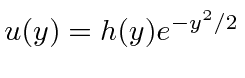 .)
We must avoid this.
.)
We must avoid this.
We can avoid the problem if the series terminates and does not go on to infinite
![]() .
.
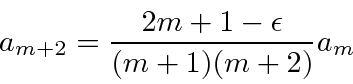
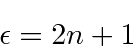
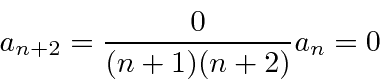
The acceptable solutions then satisfy the requirement
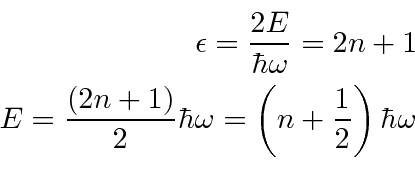
The ground state wavefunction is particularly simple, having only one term.
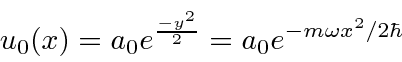
Lets find
![]() by normalizing the wavefunction.
by normalizing the wavefunction.
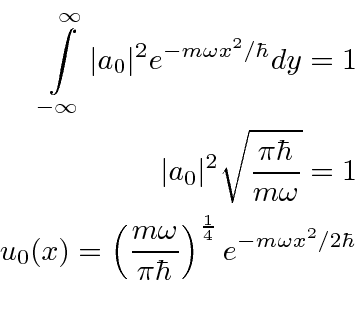
Jim Branson 2013-04-22