Next: Solving the HO Differential Up: Derivations and Computations Previous: Scattering from a 1D Contents
In the two outer regions we have solutions
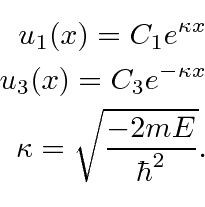
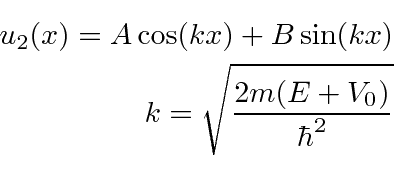
At
![]() we get
we get
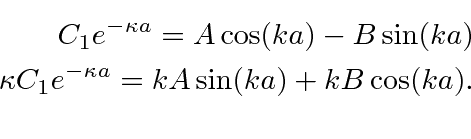
At
![]() we get
we get
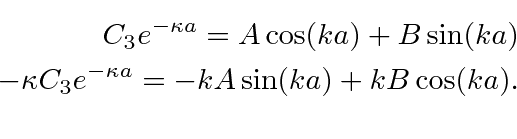
Divide these two pairs of equations to get two expressions for
![]() .
.
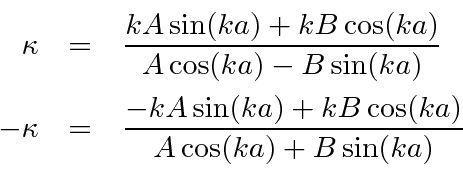
Factoring out the
![]() , we have two expressions for the same quantity.
, we have two expressions for the same quantity.
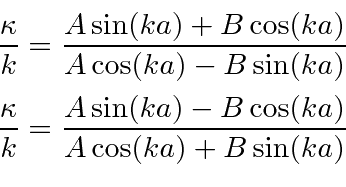
If we equate the two expressions,
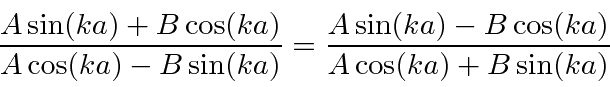
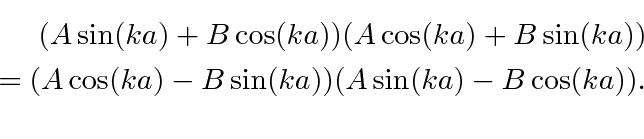
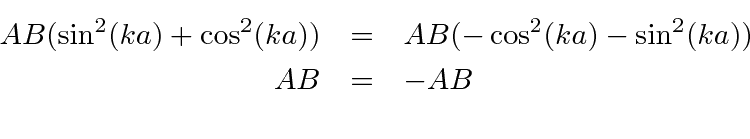
This means that the states separate into even parity and odd parity states. We could have guessed this from the potential.
Now lets use one equation.
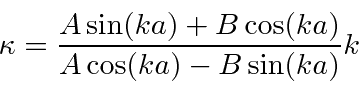
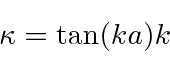
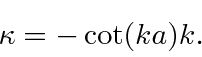
Jim Branson 2013-04-22