Next: Bound States of a Up: Derivations and Computations Previous: Probability Flux for the Contents
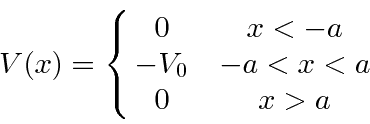
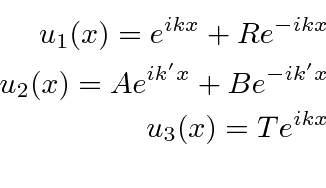
We now match the wave function and its first derivative at the two boundaries yielding 4 equations.
That's good since we have 4 constants to determine.
At
![]() we have 2 equations which we can use to eliminate
we have 2 equations which we can use to eliminate
![]() and
and
![]() .
.
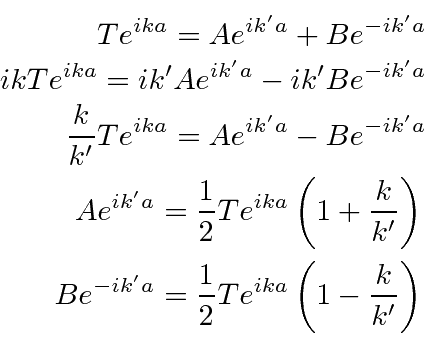
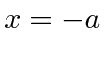 we have 2 equations which can now be written in terms of
we have 2 equations which can now be written in terms of
![\begin{eqnarray*}
e^{-ika}+Re^{ika}=Ae^{-ik'a}+Be^{ik'a} \\
ike^{-ika}-ikRe^{ik...
...\right)e^{-2ik'a}-\left({k'\over k}-1\right)e^{2ik'a}\right] \\
\end{eqnarray*}](img1327.png)
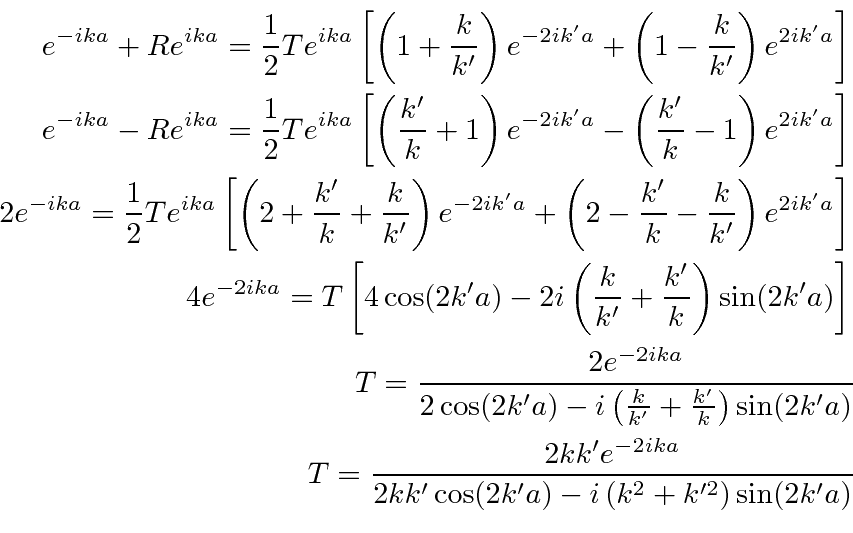
We can subtract the same equations to most easily solve for
![]() .
.
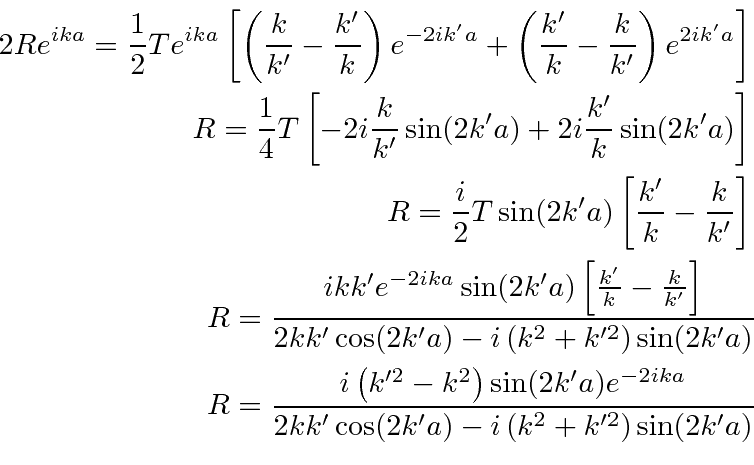
We have solved the boundary condition equations to find the reflection and transmission amplitudes
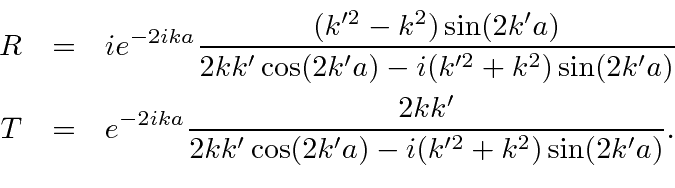
Jim Branson 2013-04-22