Next: Scattering from a 1D Up: Derivations and Computations Previous: Derivations and Computations Contents
The probability flux is given by
![\begin{displaymath}\bgroup\color{black} j(x,t)={\hbar\over 2mi}
\left[\psi^*{\pa...
...\partial x}-{\partial\psi^*\over\partial x}\psi\right] .\egroup\end{displaymath}](img1319.png)
We can save some effort by noticing that this contains an expression minus its complex conjugate.
(This assures that term in brackets is imaginary and the flux is then real.)
![\begin{displaymath}\bgroup\color{black} j={\hbar\over 2im}\left[u^*{du\over dx}-...
...\right]={\hbar\over 2im}\left[u^*{du\over dx}-CC\right] \egroup\end{displaymath}](img1320.png)
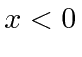
![\begin{eqnarray*}
j&=&{\hbar\over 2im}[(e^{-ikx}+R^*e^{ikx})(ike^{ikx}-ikRe^{-ik...
...2ikx}-R^*R] + CC \\
j&=&[1-\vert R\vert^2]{\hbar k\over m} .\\
\end{eqnarray*}](img1321.png)
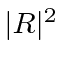 as we said.
For
as we said.
For
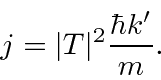
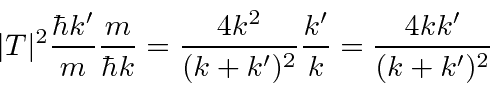
Jim Branson 2013-04-22