Next: The Delta Function Model Up: One Dimensional Potentials Previous: The Delta Function Potential Contents
The use of two delta functions allows us to see, to some extent,
how atoms bind into molecules.
Our potential is
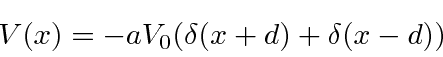
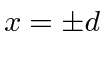 .
This is a parity symmetric potential, so we can assume that our solutions will be parity eigenstates.
.
This is a parity symmetric potential, so we can assume that our solutions will be parity eigenstates.
For even parity, our solution in the three regions is
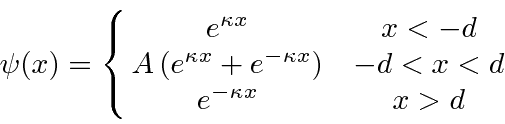
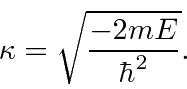
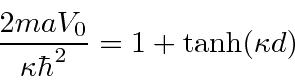
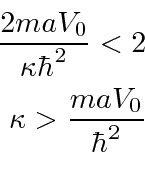
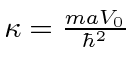 for the single delta function,
this
for the single delta function,
this
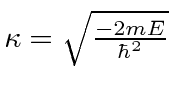 is larger than the one for the single
delta function.
This means that
is larger than the one for the single
delta function.
This means that
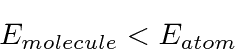
The figure below shows the two solutions plotted on the same graph as the potential.
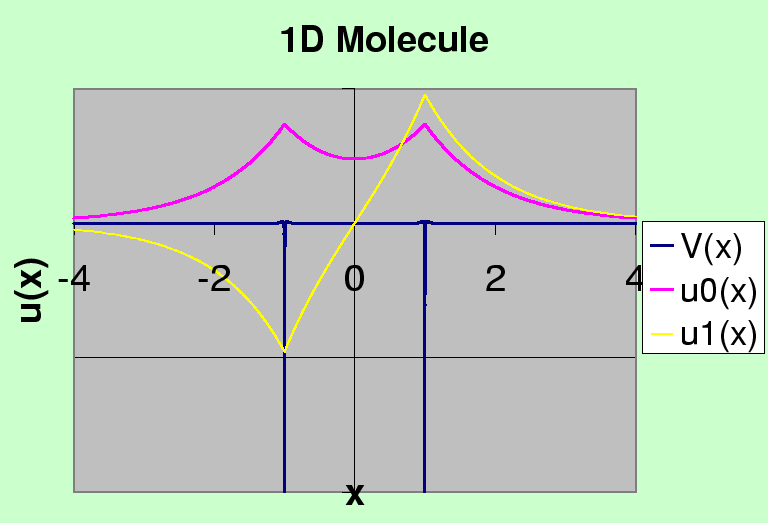
Two Hydrogen atoms bind together to form a molecule with a separation of 0.74 Angstroms,
just larger than the Bohr radius of 0.53 Angstroms.
The binding energy (for the two electrons) is about 4.5 eV.
If we approximate the Coulomb potential by with a delta function, setting
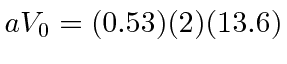 eV Angstroms,
our very naive calculation would give 1.48 eV for one electron, which is at least the right order of magnitude.
eV Angstroms,
our very naive calculation would give 1.48 eV for one electron, which is at least the right order of magnitude.
The odd parity solution has an energy that satisfies the equation
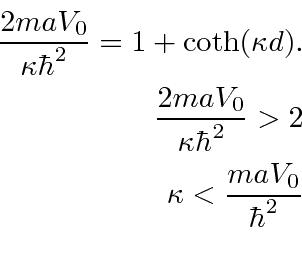
Jim Branson 2013-04-22