The Delta Function Potential *

Take a simple, attractive delta function potential and look for the bound states.

$$\bgroup\color{black} V(x)=-aV_0\delta(x)\egroup$$

These will have energy less than zero so the solutions are

$$\bgroup\color{black} \psi(x)=\left\{ \matrix{Ae^{\kappa x} & x<0 \cr Ae^{-\kappa x} & x>0\cr} \right. \egroup$$

where

$$\bgroup\color{black} \kappa=\sqrt{-2mE\over\hbar^2} .\egroup$$

There are only two regions, above and below the delta function. We don't need to worry about the one point at $x=0$ - the two solutions will match there. We have already made the wave function continuous at $x=0$ by using the same coefficient, $A$, for the solution in both regions.

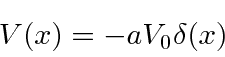
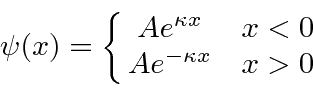
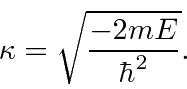
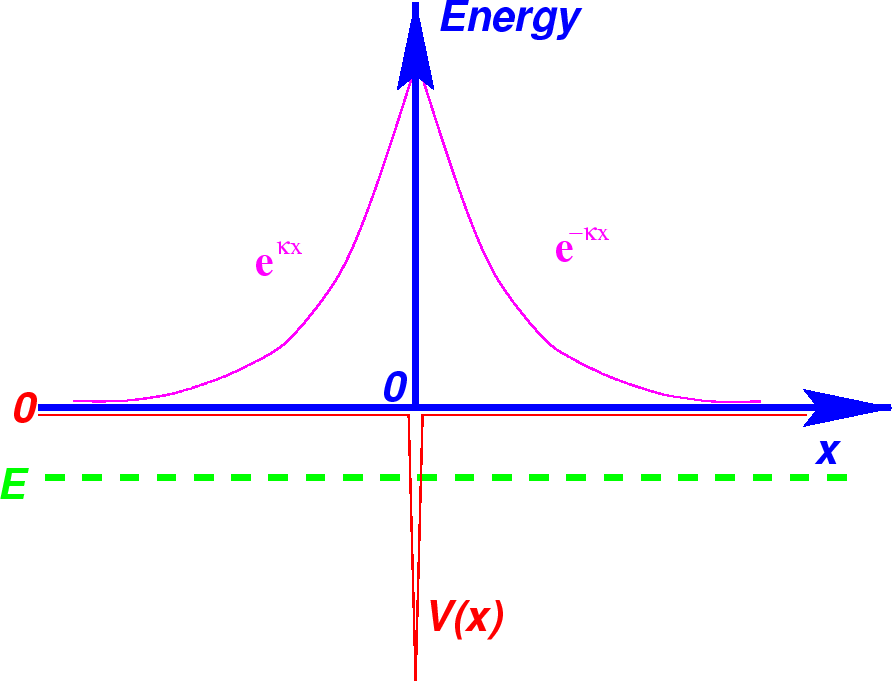
We now need to meet the boundary condition on the first derivative at $x=0$. Recall that the delta function causes a known discontinuity in the first derivative.

$$\begin{eqnarray*} \left.{d\psi\over dx}\right\vert _{+\epsilon}-\left.{d\psi\ove... ...kappa = -{2maV_0\over\hbar^2} \\ \kappa={maV_0\over\hbar^2} \\ \end{eqnarray*}$$

Putting in the formula for $\kappa$ in terms of the energy.

$$\begin{eqnarray*} {-2mE\over\hbar^2}={m^2a^2V_0^2\over\hbar^4} \\ E=-{ma^2V_0^2\over 2\hbar^2} \\ \end{eqnarray*}$$

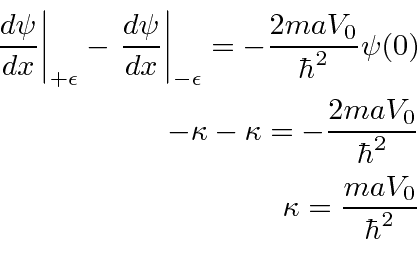
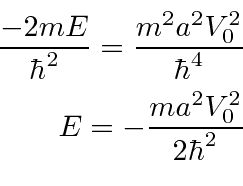
There is only one energy for which we can satisfy the boundary conditions. There is only one bound state in an attractive delta function potential.