Next: The Delta Function Potential Up: One Dimensional Potentials Previous: The Potential Barrier Contents
The harmonic oscillator is an extremely important physics problem. Many potentials look like a harmonic oscillator near their minimum. This is the first non-constant potential for which we will solve the Schrödinger Equation.
The harmonic oscillator Hamiltonian is given by
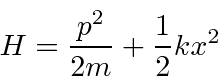
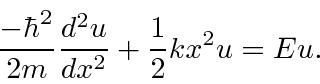
It is standard to remove the spring constant
![]() from the Hamiltonian,
replacing it with the classical oscillator frequency.
from the Hamiltonian,
replacing it with the classical oscillator frequency.
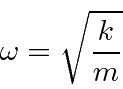
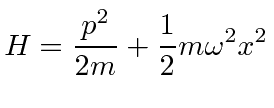 |
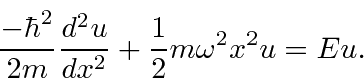
To
solve the Harmonic Oscillator equation,
we will first change to dimensionless variables,
then find the form of the solution for
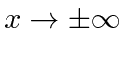 , then
multiply that solution by a polynomial, derive a recursion relation
between the coefficients of the polynomial, show that the polynomial series
must terminate if the solutions are to be normalizable, derive the energy
eigenvalues, then finally derive the functions that are solutions.
, then
multiply that solution by a polynomial, derive a recursion relation
between the coefficients of the polynomial, show that the polynomial series
must terminate if the solutions are to be normalizable, derive the energy
eigenvalues, then finally derive the functions that are solutions.
The energy eigenvalues are
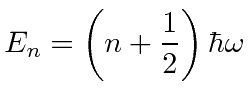 |
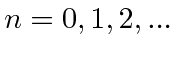 .
There are a countably infinite number of solutions with equal energy spacing.
We have been forced to have quantized energies by the requirement that the
wave functions be normalizable.
.
There are a countably infinite number of solutions with equal energy spacing.
We have been forced to have quantized energies by the requirement that the
wave functions be normalizable.
The ground state wave function is.
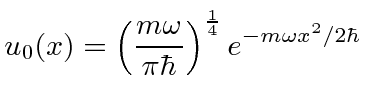 |
The first excited state is an odd parity state, with a first order polynomial multiplying the same Gaussian.
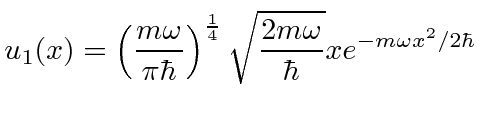 |
The second excited state is even parity, with a second order polynomial multiplying the same Gaussian.
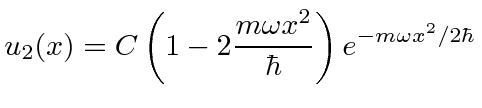 |
Note that
![]() is equal to the number of zeros of the wavefunction.
This is a common trend.
With more zeros, a wavefunction has more curvature and hence more kinetic energy.
is equal to the number of zeros of the wavefunction.
This is a common trend.
With more zeros, a wavefunction has more curvature and hence more kinetic energy.
The general solution can be written as
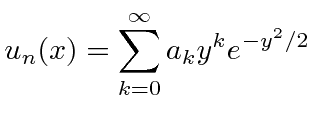 |
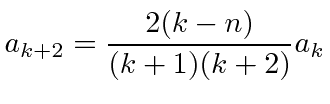 |
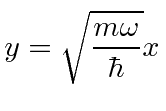 |
Jim Branson 2013-04-22