The Potential Barrier

With an analysis of the Potential Barrier problem, we can understand the phenomenon of quantum tunneling.

$$\bgroup\color{black} V(x)=\left\{ \matrix{0 & x<-a \cr +V_0 & -a<x<a \cr 0& x>a\cr} \right. \egroup$$

Numbering the three regions from left to right,

$$\begin{eqnarray*} u_1(x)=e^{ikx}+Re^{-ikx} \\ u_2(x)=Ae^{\kappa x}+Be^{-\kappa x} \\ u_3(x)=Te^{ikx} \\ \end{eqnarray*}$$

Again we assume a beam of definite momentum incident from the left and no wave incident from the right. For the solutions outside the barrier,

$$\bgroup\color{black} k=\sqrt{2mE\over\hbar^2} .\egroup$$

Inside the barrier,

$$\bgroup\color{black} \kappa=\sqrt{2m(V_0-E)\over\hbar^2} .\egroup$$

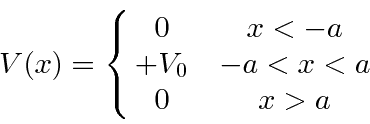
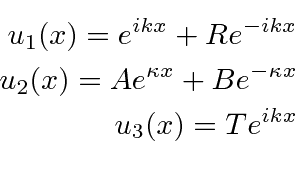
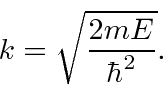
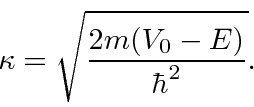
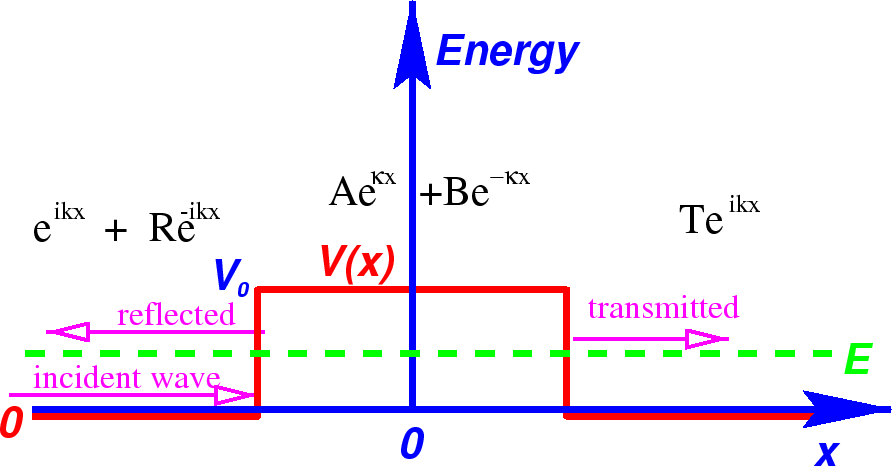
This is actually the same as the (unbound) potential well problem with the substitution

$$\bgroup\color{black} k'\rightarrow i\kappa \egroup$$

in the center region.

The amplitude to be transmitted is

$$\bgroup\color{black} T=e^{-2ika}{2k\kappa\over 2k\kappa\cosh(2\kappa a)-i(k^2-\kappa^2)\sinh(2\kappa a)} .\egroup$$

We can compute the probability to be transmitted.

$$\bgroup\color{black} \vert T\vert^2={(2k\kappa)^2\over (k^2+\... ...ft({4k\kappa\over k^2+\kappa^2}\right)^2 e^{-4\kappa a} \egroup$$

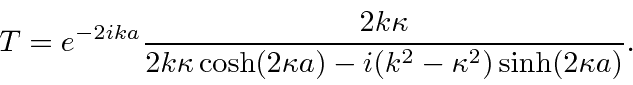
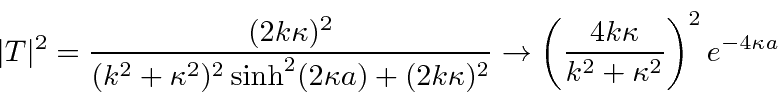
An approximate probability is sometimes useful.

$$\bgroup\color{black}\vert T\vert^2\approx e^{-2\kappa (2a)}=e^{-2\int\limits_{-a}^a \sqrt{{2m\over\hbar^2}[V(x)-E]}}dx \egroup$$

Classically the transmission probability would be zero. In Quantum Mechanics, the particle is allowed to violate energy conservation for a short timeand so has a chance to tunnel through the barrier.

Tunneling can be applied to cold emission of electrons from a metal, alpha decay of nuclei, semiconductors, and many other problems.