Next: Examples Up: More Fun with Operators Previous: The Time Development Operator Contents
To begin, lets compute the expectation value of an operator
![]() .
.
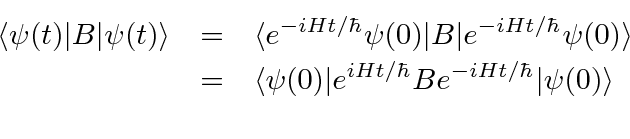
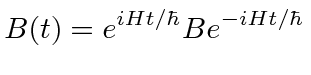 |
This is called the Heisenberg Picture. In it, the operators evolve with time and the wavefunctions remain constant.
The usual Schrödinger picture has the states evolving and the operators constant.
We can now compute the time derivative of an operator.
![\begin{eqnarray*}
{d\over dt}B(t)&=&{iH\over\hbar}e^{iHt/\hbar}Be^{-iHt/\hbar}-e...
...\hbar}e^{iHt/\hbar}[H,B]e^{-iHt/\hbar}={i\over\hbar}[H,B(t)] \\
\end{eqnarray*}](img1557.png)
As an example, we may look at the HO operators
![]() and
and
![]() .
We have already computed the commutator.
.
We have already computed the commutator.
![\begin{eqnarray*}[H,A]=-\hbar\omega A \\
{dA\over dt}=-{i\over\hbar}\hbar\omega A=-i\omega A \\
\end{eqnarray*}](img1558.png)
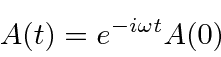
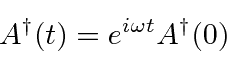
We can combine these to get the momentum and position operators in the Heisenberg picture.
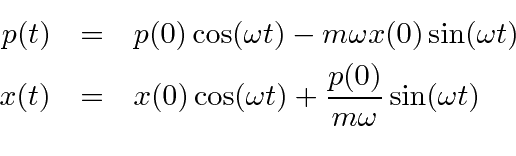
Jim Branson 2013-04-22