Next: The Heisenberg Picture * Up: More Fun with Operators Previous: Time Derivative of Expectation Contents
We can actually make an operator that does the time development of a wave function. We just make the simple exponential solution to the Schrödinger equation using operators.
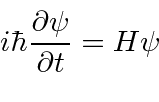
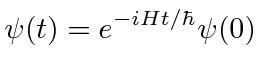 |
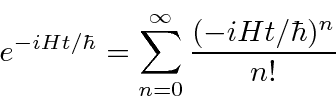
![]() is the time development operator.
It takes a state from time 0 to time
is the time development operator.
It takes a state from time 0 to time
![]() .
.