Time Derivative of Expectation Values *

We wish to compute the time derivative of the expectation value of an operator $A$ in the state $\psi$. Thinking about the integral, this has three terms.

$$\begin{eqnarray*} {d\over dt}\left\langle\psi\left\vert A\right\vert\psi\right\r... ...\vert{\partial A\over\partial t}\right\vert\psi\right\rangle \\ \end{eqnarray*}$$

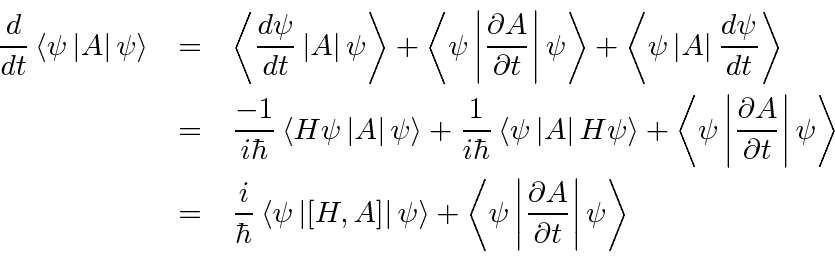
This is an important general result for the time derivative of expectation values.

$${d\over dt}\left\langle\psi\left\vert A\right... ...le\psi\left\vert{\partial A\over\partial t}\right\vert\psi\right\rangle$$

which becomes simple if the operator itself does not explicitly depend on time.

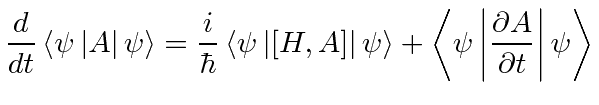$$\bgroup\color{black}{d\over dt}\left\langle\psi\left\vert A\r... ...t\langle\psi\left\vert[H,A]\right\vert\psi\right\rangle \egroup$$

Expectation values of operators that commute with the Hamiltonian are constants of the motion.

We can apply this to verify that the expectation value of $x$ behaves as we would expect for a classical particle.

$${d\left\langle x\right\rangle\over dt}={i\ove... ...p^2\over 2m},x\right]\right\rangle =\left\langle{p\over m}\right\rangle$$

This is a good result. This is called the Ehrenfest Theorem.

For momentum,

$${d\langle p\rangle\over dt}={i\over\hbar}\lef... ...er dx}\right]\right\rangle =-\left\langle{dV(x)\over dx} \right\rangle$$

which Mr. Newton told us a long time ago.