Next: Time Derivative of Expectation Up: More Fun with Operators Previous: A Complete Set of Contents
Let us now derive the uncertainty relation for non-commuting operators
![]() and
and
![]() .
First, given a state
.
First, given a state
![]() ,
the Mean Square uncertainty
in the physical quantity represented is defined as
,
the Mean Square uncertainty
in the physical quantity represented is defined as
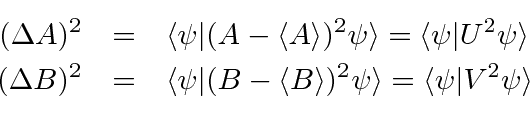
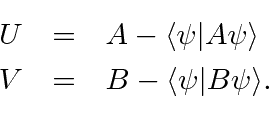
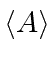 and
and
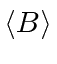 are just constants, notice that
are just constants, notice that
![\begin{displaymath}\bgroup\color{black} [U,V]=[A,B] \egroup\end{displaymath}](img1538.png)
Now we will dot
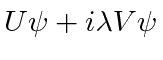 into itself to get some information about
the uncertainties.
The dot product must be greater than or equal to zero.
into itself to get some information about
the uncertainties.
The dot product must be greater than or equal to zero.
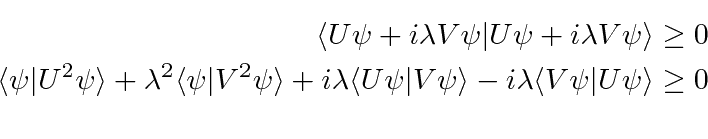
![\begin{displaymath}\bgroup\color{black} (\Delta A)^2+\lambda^2(\Delta B)^2+i\lambda\langle\psi\vert[U,V]\vert\psi\rangle\geq 0 \egroup\end{displaymath}](img1541.png)
![\begin{eqnarray*}
{\partial\over\partial\lambda}=0 \\
2\lambda(\Delta B)^2+i\la...
...{-i\langle\psi\vert[U,V]\vert\psi\rangle\over 2(\Delta B)^2} \\
\end{eqnarray*}](img1542.png)
Plug in that
![]() .
.
![\begin{eqnarray*}
(\Delta A)^2-{1\over 4}{\langle\psi\vert[U,V]\vert\psi\rangle^...
...\rangle^2
=\langle\psi\vert{i\over 2}[U,V]\vert\psi\rangle^2 \\
\end{eqnarray*}](img1543.png)
This result is the uncertainty for non-commuting operators.
![\bgroup\color{black}$\displaystyle (\Delta A)(\Delta B)\geq{i\over 2}\langle[A,B]\rangle $\egroup](img1544.png) |
![\bgroup\color{black}$[p,x]$\egroup](img1025.png) ,
the expectation values can be removed.
,
the expectation values can be removed.
![\begin{displaymath}\bgroup\color{black} (\Delta A)(\Delta B)\geq{i\over 2}[A,B] \egroup\end{displaymath}](img1545.png)
For momentum and position, this agrees with the uncertainty principle we know.
![\bgroup\color{black}$\displaystyle (\Delta p)(\Delta x)\geq{i\over 2}\langle[p,x]\rangle={\hbar\over 2} $\egroup](img1546.png) |
(Note that we could have simplified the proof by just stating that we choose to dot
![\bgroup\color{black}$(U+{i\langle[U,V]\rangle\over 2(\Delta B)^2}V)\psi$\egroup](img1547.png) into itself and require that its positive.
It would not have been clear that this was the strongest condition we could get.)
into itself and require that its positive.
It would not have been clear that this was the strongest condition we could get.)
Jim Branson 2013-04-22