Next: Identical Particles Up: Course Summary Previous: More Fun with Operators Contents
So far we have been working with states of just one particle in one dimension.
The
extension to two different particles and to three dimensions
is straightforward.
The coordinates and momenta of different particles and of the additional dimensions
commute with each other as we might expect from classical physics.
The only things that don't commute are a coordinate with its momentum, for example,
![\begin{displaymath}\bgroup\color{black}[p_{(2)z},z_{(2)}]={\hbar\over i}\egroup\end{displaymath}](img209.png)
![\begin{displaymath}\bgroup\color{black}[p_{(1)x},x_{(2)}]=[p_{(2)z},y_{(2)}]=0.\egroup\end{displaymath}](img210.png)
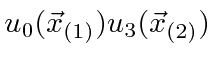 ,
or we may write states in which the particles are correlated.
The Hamiltonian for two particles in 3 dimensions simply becomes
,
or we may write states in which the particles are correlated.
The Hamiltonian for two particles in 3 dimensions simply becomes
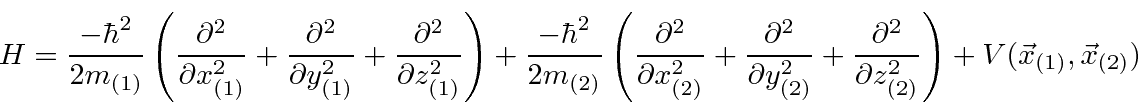
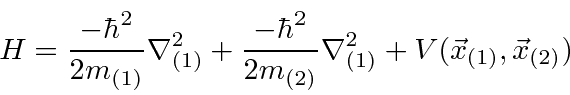
If two particles interact with each other, with no external potential,
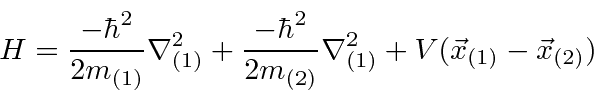
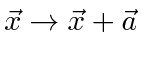 .
We can show that this
translational symmetry
implies conservation of total momentum.
Similarly, we will show that rotational symmetry implies conservation of
angular momentum,
and that time symmetry implies conservation of energy.
.
We can show that this
translational symmetry
implies conservation of total momentum.
Similarly, we will show that rotational symmetry implies conservation of
angular momentum,
and that time symmetry implies conservation of energy.
For two particles interacting through a potential that depends only on difference on the coordinates,
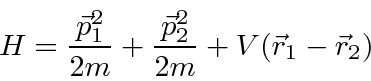
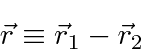
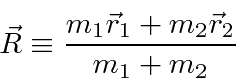
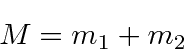
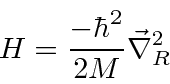
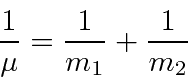
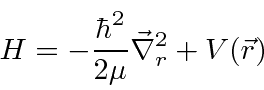
Jim Branson 2013-04-22