Next: Some 3D Problems Separable Up: Course Summary Previous: Two Particles in 3 Contents
Identical particles present us with another symmetry in nature.
Electrons, for example, are indistinguishable from each other so we must have
a
symmetry of the Hamiltonian under interchange
of any pair of electrons.
Lets call the operator that interchanges electron-1 and electron-2
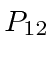 .
.
![\begin{displaymath}\bgroup\color{black}[H,P_{12}]=0\egroup\end{displaymath}](img224.png)
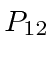 .
Its easy to see (by operating on an eigenstate twice with
.
Its easy to see (by operating on an eigenstate twice with
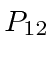 ),
that the possible eigenvalues are
),
that the possible eigenvalues are